��Ŀ����
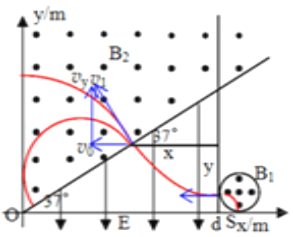
����Ŀ����ͼ��ʾ��ֱ��![]() ��y��֮���д�ֱ��xOyƽ���������ǿ�ų�B2��ֱ��x��d��
��y��֮���д�ֱ��xOyƽ���������ǿ�ų�B2��ֱ��x��d��![]() ������y�Ḻ�������ǿ�糡���糡ǿ��
������y�Ḻ�������ǿ�糡���糡ǿ��![]() ������һ�뾶R=
������һ�뾶R=![]() m��Բ����ǿ�ų����Ÿ�Ӧǿ��B1=
m��Բ����ǿ�ų����Ÿ�Ӧǿ��B1=![]() ������ֱ����ƽ�����⣬��Բ��ֱ��x��d��x������У�����x��������S�㡣һ����������Ӵ�S����y������������ٶ�v0����Բ�δų�������һ��ʱ�����ų�����B2���ҵ�һ�ν���ų�B2ʱ���ٶȷ�����ֱ��
������ֱ����ƽ�����⣬��Բ��ֱ��x��d��x������У�����x��������S�㡣һ����������Ӵ�S����y������������ٶ�v0����Բ�δų�������һ��ʱ�����ų�����B2���ҵ�һ�ν���ų�B2ʱ���ٶȷ�����ֱ��![]() ��ֱ�������ٶȴ�Сv0��1.0��105m/s�����ӵıȺ�Ϊ
��ֱ�������ٶȴ�Сv0��1.0��105m/s�����ӵıȺ�Ϊ![]() =5.0��105C/kg�������������ơ���
=5.0��105C/kg�������������ơ���

(1)������Բ����ǿ�ų����˶���ʱ��t1��
(2)����d��ֵ��
(3)Ҫʹ�������˶���x��ĸ����ᣬ��Ÿ�Ӧǿ��B2Ӧ���������
���𰸡�(1)2.6��10��6s(2)4m(3)0��B2��0.13T����B2��0.3T
��������
(1)�ڴų�B1��
![]()
���
![]()
�����켣ǡΪ�ķ�֮һԲ��
![]()
��
![]()
(2)�ڵ糡����ƽ���˶�
![]()
![]()
���
![]()
�ָ���
x=v0t
![]()
���
![]()
��������d��ֵ
![]()
(3)����ų�B2���ٶ�Ϊ��
![]()
���������ӳ��ų���y�ᴹֱʱ��Բ�ܰ뾶
![]()
�ɵ�
![]()
����
0��B2��0.13T��
���������ӳ��ų���y������ʱ��Բ�ܰ뾶
![]()
�ɵ�
B2��0.3T
����
B2��0.3T��

��ϰ��ϵ�д�
 �����ߴ���ϵ�д�
�����ߴ���ϵ�д�
�����Ŀ





