题目内容
如图所示,在同一竖直平面内有两个正对着的半圆形光滑轨道,轨道的半径都是R。轨道端点所在的水平线相隔一定的距离x。一质量为m的小球能在其间运动而不脱离轨道,经过最低点B时的速度为v。小球在最低点B与最高点A对轨道的压力之差为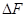 (
(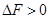 )。不计空气阻力。则:
)。不计空气阻力。则: 
A.m、x一定时,R越大,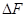 一定越大 一定越大 |
B.m、x一定时,v越大,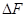 一定越大 一定越大 |
C.m、R一定时,x越大,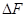 一定越大 一定越大 |
D.m、R一定时,v越大,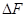 一定越大 一定越大 |
C
解析试题分析:设m在A点时的速度为 ,在B点时速度为
,在B点时速度为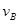 ;对m从A到B点时,根据动能定理有:
;对m从A到B点时,根据动能定理有: ,对m在B点时,受重力和支持力
,对m在B点时,受重力和支持力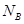 的作用,根据牛顿第二定律:
的作用,根据牛顿第二定律: ,所以
,所以 ;对m在A点,受重力和支持力
;对m在A点,受重力和支持力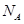 ,根据牛顿第二定律:
,根据牛顿第二定律: ,所以
,所以 ,小球在最低点B与最高点A对轨道的压力之差
,小球在最低点B与最高点A对轨道的压力之差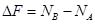 ,解得:
,解得: ,从推导的关系式可知,R越大,
,从推导的关系式可知,R越大,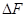 应该是越小,所以A错误,
应该是越小,所以A错误,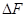 与速度
与速度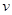 没关系,所以选项B、D都错误。 m、R一定时,当x变大时,从关系式中不难发现
没关系,所以选项B、D都错误。 m、R一定时,当x变大时,从关系式中不难发现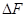 一定越大,所以C选项正确。
一定越大,所以C选项正确。
考点:本题考查了圆周运动的向心力、动能定理。

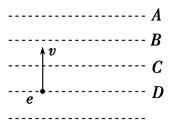
如图所示,a.b.c.d为匀强电场中的四个等势面,一个电子射入电场后的运动轨迹如实线MN所示,由此可知( )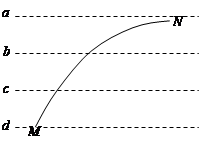
| A.电子在N的动能大于在M的动能 |
| B.电子在N的电势能小于在M的电势能 |
| C.电场强度方向向左 |
| D.电场中,a点电势低于b点电势 |
一水平放置的平行板电容器的两极扳间距为d,极扳分别与电池两极相连.上极板中心有一小孔(小孔对电场的影响可忽略不计)。小孔正上方d/2处的P点有一带电粒子,该粒子从静止开始下落.经过小孔进入电容器,并在下极板处未与极扳接触、返回。若将下极板向上平移d/3,则从P点开始下落的相同粒子将( )
| A.打到下极扳上 |
| B.在下极板处返回 |
| C.在距上极板d/2处返回 |
| D.在距上极扳2d/5处返回 |
篮球从高处释放,在重力和空气阻力的作用下加速下降过程,正确的是
| A.合力对篮球做的功等于篮球动能的增加量 |
| B.重力对篮球做的功等于篮球重力势能的减少量 |
| C.篮球重力势能的减少量等于动能的增加量 |
| D.篮球克服空气阻力所做的功等于篮球机械能的减少量 |
一个初动能为EK的带电粒子,以速率v垂直电场线方向飞入带电的平行板电容器,飞出时带电粒子动能为飞入时动能的2倍。如果使粒子的初速度为原来的2倍,那么当它飞出电容器的时刻,动能为 ( )
| A.4EK | B.4.25EK | C.5EK | D.8EK |
2012年伦敦奥运会跳水比赛首先进行的女子单人3米板比赛中,中国队派出了夺得双人项目金牌的吴敏霞和何姿。最终,吴敏霞以总分414分摘金。现假设她的质量为m,她进入水中后受到水的阻力而做减速运动,设水对她的阻力大小恒为F,那么在她减速下降高度为h的过程中,下列说法正确的是(g为当地的重力加速度) ( )
| A.她的动能减少了Fh |
| B.她的重力势能减少了mgh |
| C.她的机械能减少了(F-mg)h |
| D.她的机械能减少了Fh |
质量为m的物体,从静止开始以3g/4的加速度竖直向下运动了h,以下判断中正确的是
| A.物体的机械能减少了mgh/4 |
| B.物体的动能增加了mgh/4 |
| C.物体的重力势能减少了3mgh/4 |
| D.物体的重力势能增加了mgh |