题目内容
如图所示，半径为R、内径很小的光滑半圆管置于竖直平面内，两个质量均为m的小球A、B，以不同的速度进入管内，A通过最高点C时，对管壁上部的压力为3mg，B通过最高点C时，对管壁下部的压力为0．75mg，求A、B两球落地点间的距离。
3R
解析试题分析：两个小球在最高点时，受重力和管壁的作用力，这两个力的合力作为向心力，离开轨道后两球均做平抛运动，A、B两球落地点间的距离等于它们平抛运动的水平位移之差。
对A球：3mg+mg=m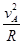
（2分） vA=
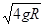（1分）
对B球：mg－0.75mg=m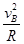
（2分） vB=
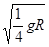（1分）
由平抛运动规律可得落地时它们的水平位移为：sA=vAt=vA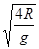
="4" R （2分）
sB=vBt=vB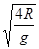=R （1分） ∴sA－sB=3R （1分）
考点：考查圆周运动的应用，
点评：a球在最高点由支持力和重力的合力提供向心力，由此求得A球速度，同理可求得B球速度，经过最高点后两球做平抛运动，由竖直高度求得时间，再由水平方向的匀速直线运动求得位移差
练习册系列答案
精英口算卡系列答案
相关题目
（2006?淮北模拟）如图所示，半径为R，内径很小的光滑半圆管竖直放置．两个质量均为m的小球a、b以不同的速度进入管内，a通过最高点A时，对管壁上部的压力为3mg，b通过最高点A时，对管壁下部的压力为0.75mg，求a、b两球落地点间的距离．
如图所示，半径为R 的光滑圆形轨道竖直固定放置，质量为m 的小球在圆形轨道内侧做圆周运动．小球通过轨道最高点时恰好与轨道间没有相互作用力．已知当地的重力加速度大小为g，不计空气阻力．试求：
如图所示，半径为R的圆筒绕竖直中心轴OO′转动，小物块A靠在圆筒的内壁上，它与圆筒的动摩擦因数为μ（认为最大静摩擦力等于滑动摩擦力），现要使A不下落，则圆筒转动的角速度ω至少为（ ）
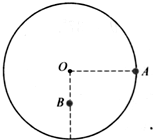如图所示，半径为R，质量不计的圆盘盘面与地面相垂直，圆心处有一个垂直盘面的光滑水平固定轴O，在盘的最右边缘处固定一个质量为m的小球A，在O点的正下方离O点R/2处固定一个质量也为m的小球B，放开盘让其自由转动，问：