题目内容
 (2006?淮北模拟)如图所示,半径为R,内径很小的光滑半圆管竖直放置.两个质量均为m的小球a、b以不同的速度进入管内,a通过最高点A时,对管壁上部的压力为3mg,b通过最高点A时,对管壁下部的压力为0.75mg,求a、b两球落地点间的距离.
(2006?淮北模拟)如图所示,半径为R,内径很小的光滑半圆管竖直放置.两个质量均为m的小球a、b以不同的速度进入管内,a通过最高点A时,对管壁上部的压力为3mg,b通过最高点A时,对管壁下部的压力为0.75mg,求a、b两球落地点间的距离.分析:对两个球分别受力分析,根据合力提供向心力,求出速度,此后球做平抛运动,正交分解后,根据运动学公式列式求解即可.
解答:解:两个小球在最高点时,受重力和管壁的作用力,这两个力的合力作为向心力,离开轨道后两球均做平抛运动,A、B两球落地点间的距离等于它们平抛运动的水平位移之差.
对A球:3mg+mg=m
解得
vA=
对B球:mg-0.75mg=m
解得
vB=
由平抛运动规律可得落地时它们的水平位移为:
sA=vAt=vA
=4R
sB=vBt=vB
=R
∴sA-sB=3R
即a、b两球落地点间的距离为3R.
对A球:3mg+mg=m
| ||
| R |
解得
vA=
| 4gR |
对B球:mg-0.75mg=m
| ||
| R |
解得
vB=
|
由平抛运动规律可得落地时它们的水平位移为:
sA=vAt=vA
|
sB=vBt=vB
|
∴sA-sB=3R
即a、b两球落地点间的距离为3R.
点评:本题关键是对小球在最高点处时受力分析,然后根据向心力公式和牛顿第二定律求出平抛的初速度,最后根据平抛运动的分位移公式列式求解.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
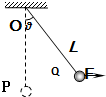 (2006?淮北模拟)一质量为m的小球,用长为L的轻绳悬挂于O点,小球 在水平力F作用下,从平衡位置P很缓慢地移动到Q点,如图所示,则力F所做的功为( )
(2006?淮北模拟)一质量为m的小球,用长为L的轻绳悬挂于O点,小球 在水平力F作用下,从平衡位置P很缓慢地移动到Q点,如图所示,则力F所做的功为( )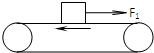 (2006?淮北模拟)如图所示,皮带是水平的,当皮带不动时,为使物体向右匀速运动而作用在物体上的水平拉力为F1;当皮带向左运动时,为使物体向右匀速运动而作用在物体上的水平力为F2,则( )
(2006?淮北模拟)如图所示,皮带是水平的,当皮带不动时,为使物体向右匀速运动而作用在物体上的水平拉力为F1;当皮带向左运动时,为使物体向右匀速运动而作用在物体上的水平力为F2,则( )