题目内容
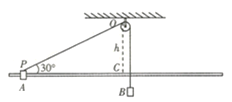
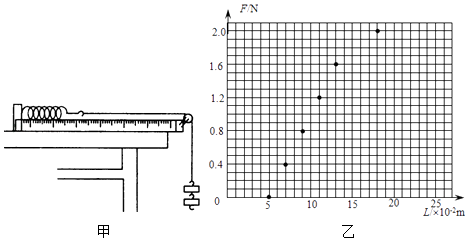
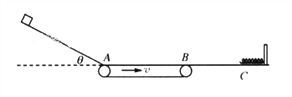
【题目】如图所示，水平传送带左端A处与倾角为
=37°的光滑斜面平滑连接，右端B处与一水平面平滑连接，水平面上有一固定竖直挡板，挡板左侧与一轻弹簧连接，弹簧处于自然状态，弹簧左端刚好与水平面上的C点对齐，斜面长为x1=3 m，传送带长L=2 m，BC段长x2=1 m，传送带以速度v=2 m／s顺时针转动．一质量为1 kg的物块从斜面顶端由静止释放，已知物块与传送带间及水平面BC段的动摩擦因数
0.2，水平面C点右侧光滑，重力加速度取g=10 m／s2，sin 37°=0.6，cos 37°=0.8，求：
(1)弹簧获得的最大弹性势能；
(2)物块第三次到达B点时的速度大小；
(3)物块与传送带由于相对滑动而产生热量的最大值．
【答案】（1）
（2）
（3）
【解析】（1）设物体滑到斜面底端的速度为v1，根据机械能守恒有：
求得：v1=6m/s
由于v1>v，因此物块滑上传送带后开始做匀减速运动，加速度大小为
设物块在传送带上先减速后匀速，则减速运动的位移：
由于s1>L，假设不成立，物块在传送带上一直匀减速，根据功能关系：
（2）设物块第三次到达A点的速度为v2，根据功能关系：
求得：v2=
m/s
物块以 的速度第三次滑上传送带，由于
因此物块第三次滑上传送带一直做匀减速运动，第三次到达B点速度刚好等于2m/s。
（3）由于
因此物块不会第四次滑上传送带。根据能量转化与守恒定律，物块由于与传送带摩擦而产生的热量为：
带入数据得：Q=12J
练习册系列答案
相关题目
