题目内容
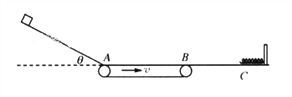
【题目】如图所示，水平光滑长杆上套有小物块A，细线跨过位于O点的轻质光滑定滑轮，一端连接A，另一端悬挂小物块B，物块A、B质量相等。C为O点正下方杆上的点，滑轮到杆的距离OC=h. 开始时A位于P点，PO与水平方向的夹角为30°。现将A、B静止释放。则下列说法正确的是（ ）
A. 物块A由P点出发第一次到达C点过程中，速度先增大后减小
B. 物块A经过C点时的速度大小为
C. 物块A在杆上长为
的范围内做往复运动
D. 在物块A由P点出发第一次到达C点过程中，物块B克服细线拉力做的功等于B重力势能的减少量
【答案】BCD
【解析】A. 物块A由P点出发第一次到达C点过程中，物块B从释放到了最低点，此过程中，对A受力分析，可知绳子的拉力一直做正功，其动能一直增大，则A的速度一直增大，A错误； B. B的机械能最小时，即为A到达C点，此时A的速度最大，设为vA，此时B的速度为0,根据系统的机械能守恒得：
，物块A.B质量相等，解得：vA=
。故B正确；
C. PC
，根据对称性，A向右能够到达的最远距离等于P、C间的距离，所以物块A在杆上长为
的范围内做往复运动，C正确；
D. 物块A由P点出发第一次到达C点的过程中，绳子对B一直做负功，其机械能一直减小，物块B初末速度都为零，根据动能定理，克服细线拉力做的功等于B重力势能的减少量，故D正确。
故选：BCD.
练习册系列答案
相关题目
