题目内容
9.有一星球其半径为地球半径的2倍,平均密度与地球相同,今把一台在地球表面走时准确的秒摆移到该星球表面,该秒摆周期变为( )| A. | 0.5S | B. | $\frac{\sqrt{2}}{2}$S | C. | $\sqrt{2}$S | D. | 2S |
分析 首先知道地球上的秒表周期为1s,再求出星球上的重力加速度,再利用单摆的振动周期公式即可求解.
解答 解:地球上秒摆的振动周期公式T=2π$\sqrt{\frac{L}{{g}_{地}}}$=1s
据星球表面重力近似等于万有引力,所以$\frac{GMm}{{R}^{2}}=mg$
又因为:M=ρV
V=$\frac{4π{R}^{3}}{3}$
秒摆在星球上振动周期公式T1=2π$\sqrt{\frac{L}{g}}$
联立以上解得:T1=$\sqrt{2}$s,故ABD错误,C正确.
故选:C.
点评 解本题需要具备以下知识:秒摆的周期为1s、单摆的振动周期公式T=2π$\sqrt{\frac{L}{g}}$、星球表面重力近似等于万有引力、体积和质量公式,此题综合性较强.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
17.关于运动的合成与分解,以下说法错误的是( )
| A. | 由两个分运动求合运动,合运动是唯一确定的 | |
| B. | 由合运动分解为两个分运动,可以有不同的分解方法 | |
| C. | 物体只有做曲线运动时,才能将这个运动分解为两个分运动 | |
| D. | 任何形式的运动,都可以用几个分运动代替 |
4.列车轨道在转弯处外轨高于内轨,其高度差由转弯半径与火车速度确定.若在某转弯处规定行驶速度为v,则下列说法中正确的是( )
| A. | 当以速度v通过此弯路时,火车重力与轨道面支持力的合力提供向心力 | |
| B. | 当以速度v通过此弯路时,火车受到的摩擦力提供向心力 | |
| C. | 当速度大于v时,轮缘侧向挤压外轨 | |
| D. | 当速度小于v时,轮缘侧向挤压外轨 |
14.如图所示,当正方形薄板绕着过其中心O并与板垂直的转动轴转动时,板上A、B两点的( )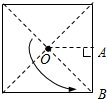

| A. | 角速度之比ωA:ωB=1:$\sqrt{2}$ | B. | 角速度之比ωA:ωB=$\sqrt{2}$:1 | ||
| C. | 线速度之比vA:vB=1:$\sqrt{2}$ | D. | 线速度之比vA:vB=$\sqrt{2}$:1 |
1.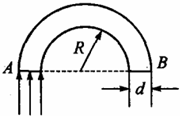 如图所示,一根粗细均匀的半圆形玻璃棒,折射率为1.5,半径为R,两端面A、B均为正方形,宽度为d.令一束平行光垂直于端面A入射,要使入射光线全都从另一端面B射出,则R与d之比的最小值应为( )
如图所示,一根粗细均匀的半圆形玻璃棒,折射率为1.5,半径为R,两端面A、B均为正方形,宽度为d.令一束平行光垂直于端面A入射,要使入射光线全都从另一端面B射出,则R与d之比的最小值应为( )
 如图所示,一根粗细均匀的半圆形玻璃棒,折射率为1.5,半径为R,两端面A、B均为正方形,宽度为d.令一束平行光垂直于端面A入射,要使入射光线全都从另一端面B射出,则R与d之比的最小值应为( )
如图所示,一根粗细均匀的半圆形玻璃棒,折射率为1.5,半径为R,两端面A、B均为正方形,宽度为d.令一束平行光垂直于端面A入射,要使入射光线全都从另一端面B射出,则R与d之比的最小值应为( )| A. | 2 | B. | 1 | C. | 3 | D. | 1.5 |
18.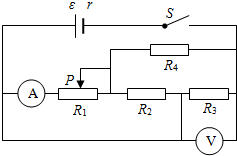 如图所示电路中,电源的内电阻为r、R1、R2、R均为定值电阻,电表均为理想电表.闭合开关S,当滑动变阻器R,的滑动触头P向右滑动时,电流表和电压表的示数变化量的大小分别为△I、△U,下列说法正确的是( )
如图所示电路中,电源的内电阻为r、R1、R2、R均为定值电阻,电表均为理想电表.闭合开关S,当滑动变阻器R,的滑动触头P向右滑动时,电流表和电压表的示数变化量的大小分别为△I、△U,下列说法正确的是( )
 如图所示电路中,电源的内电阻为r、R1、R2、R均为定值电阻,电表均为理想电表.闭合开关S,当滑动变阻器R,的滑动触头P向右滑动时,电流表和电压表的示数变化量的大小分别为△I、△U,下列说法正确的是( )
如图所示电路中,电源的内电阻为r、R1、R2、R均为定值电阻,电表均为理想电表.闭合开关S,当滑动变阻器R,的滑动触头P向右滑动时,电流表和电压表的示数变化量的大小分别为△I、△U,下列说法正确的是( )| A. | 电流表示数变大 | B. | 电压表示数变大 | C. | $\frac{△U}{△I}$<r | D. | $\frac{△U}{△I}$>r |
19.汽车从静止开始保持加速度a作匀加速运动的最长时间为t,此后汽车的运动情况是( )
| A. | 加速为零,速变恒定 | |
| B. | 加速度逐渐减小直到为零,速度逐渐增大直到最大值后保持匀速 | |
| C. | 加速度渐减小直到为零,速度也逐渐减小直至为零 | |
| D. | 加速度逐渐增大到某一值后不变,速度逐渐增大,直到最后匀速 |

 如图所示,质量为m、电阻为R、ab边长为L的矩形金属单匝线圈竖直放置,水平虚线MN、PQ之间高度差为d,t=0时刻将线圈由图中位置由静止释放,同时在虚线之间加一方向垂直纸面向外的匀强磁场,磁感应强度B大小随时间t的变化关系为B=kt(k为已知常数):t=t1(t1未知)时,ab边进入磁场电流恰好为0;t=t2时ab边穿出磁场前的瞬间线圈加速度为0.(不计空气阻力,重力加速度为g)求:
如图所示,质量为m、电阻为R、ab边长为L的矩形金属单匝线圈竖直放置,水平虚线MN、PQ之间高度差为d,t=0时刻将线圈由图中位置由静止释放,同时在虚线之间加一方向垂直纸面向外的匀强磁场,磁感应强度B大小随时间t的变化关系为B=kt(k为已知常数):t=t1(t1未知)时,ab边进入磁场电流恰好为0;t=t2时ab边穿出磁场前的瞬间线圈加速度为0.(不计空气阻力,重力加速度为g)求: