Question

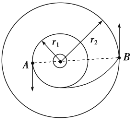
【题目】如图所示，在倾角为θ的斜面上的O点，与水平方向成60°角分别以速度v0和2v0两次抛出小球，小球先后打到斜面上的A、B两点，其中初速度是2v0的小球沿水平方向击中B点。则下列说法正确的是（　　）

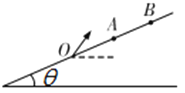
A.斜面的倾角为30°

B.击中B点的小球在空中的飞行时间为

C.初速度是v0的小球也一定沿水平方向击中A点

D.OA间的距离等于AB间的距离

Answer 1

【答案】BC

【解析】

A．研究以的速度抛出的小球的运动，反向看作平抛运动，根据几何关系可知，落到斜面上末速度与水平方向的夹角为，斜面的倾角等于位移与水平方向的夹角，根据平抛运动的规律可知，速度与水平方向夹角正切值等于位移与水平方向夹角正切值的二倍，则有

解得

则有斜面的倾角

故A错误；

B．继续反向研究击中点的小球的运动，落地斜面上的竖直速度

空中飞行的时间

故B正确；

C．落到点的小球斜上抛的水平分速度为

竖直分速度为

设飞行时间为，则有位移关系

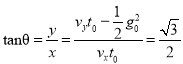
解得

小球落到点时，竖直末速度

说明小球一定沿水平方向击中点，故C正确；

D．小球落点与抛出点的距离为

即距离与初速度的平方成正比，故间的距离是间距离的4倍，间的距离等于间的距离的，故D错误；

故选BC。