题目内容
【题目】在一铅直面内有一光滑的轨道,轨道左边是光滑弧线,右边是足够长的水平直线。现有质量分别为mA和mB的两个质点,B在水平轨道上静止,A在高h处自静止滑下,与B发生弹性碰撞,碰后A仍可返回到弧线的某一高度上,并再度滑下。问:A、B的质量满足什么关系时可以至少发生两次碰撞。
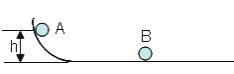
【答案】mB>3mA
【解析】
设A球与B球第一次碰撞前速度为v0,碰撞后A球和B球的速度分别为vA和vB。A球从LM轨道上下滑的过程,由机械能守恒定律得:mAgh=![]() mAv02,得:v0=
mAv02,得:v0=![]() ;对于A、B碰撞的过程,取向右为正方向,根据动量守恒定律和能量守恒定律得:
;对于A、B碰撞的过程,取向右为正方向,根据动量守恒定律和能量守恒定律得:
mAv0=mAvA+mBvB![]() mAv02=
mAv02=![]() mAvA2+
mAvA2+![]() mBvB2;
mBvB2;
解得:vA=![]() v0,vB=
v0,vB=![]() v0;
v0;
要使A、B两球至少发生两次碰撞,第一次碰撞后A球反向弹回,且A球的速度大小必须大于B球的速度。则有vA<0,且,|vA|>vB,联立解得:mB>3mA。

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目