题目内容
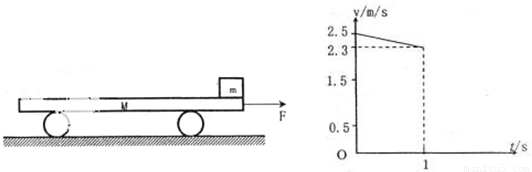
某电视台娱乐节目组在游乐园举行家庭搬运砖块比赛活动,比赛规则是:(图1)向行驶中的小车上搬放砖块,且每次只能将一块砖无初速的放到车上,车停止时立即停止搬放,以车上砖块多少决定胜负.已知每块砖质量m=0.81kg,小车上表面光滑且足够长,比赛过程中车始终受恒定牵引力F=25N作用,未放砖块时车以移v0=0.5m/s匀速前进.某家庭上场比赛时每隔T=1s搬放一块,图2中仅画出了比赛开始ls内车运动的v-t图象.(g取10m/s2)求:
(1)小车的质量及车与地面间的动摩擦因数
(2)车停止对车上放有多少砖块.

(1)小车的质量及车与地面间的动摩擦因数
(2)车停止对车上放有多少砖块.
分析:(1)开始车做匀速直线运动,知拉力和车的摩擦力相等,放上一物块后,车做匀减速运动,合力等于增加的摩擦力,根据牛顿第二定律有μmg=Ma1,以及F=μMg求出小车的质量和动摩擦因数.
(2)每放上一块砖,摩擦力都要增大,小车的合力就是增大的摩擦力,求出加速度的通项式,根据v0-a1T-a2T-a3T-…-anT≤0求出所放砖的数目.
(2)每放上一块砖,摩擦力都要增大,小车的合力就是增大的摩擦力,求出加速度的通项式,根据v0-a1T-a2T-a3T-…-anT≤0求出所放砖的数目.
解答:解:(1)开始比赛前车匀速运动,由F=μMg①
放上第一块砖后车减速运动,加速度大小为a1,由图象得a1=
=0.2m/s2②
对小车由牛顿第二定律:μmg=Ma1③
由①②③式联立解得:M=10kg④
μ=0.25⑤
(2)放上第一块砖后1s,车的速度为v1,加速度为a1v1=v0-a1T⑥
a1=
放上第二块砖后1s车的速度为v2=v1-a2T
a2=
同理v3=v2-a3T
放上第n块砖作用1s后车速为vn,加速度为anvn=vn-1-anT⑦
an=
⑧
由以上各式可得vn=v0-(a1+a2+…+an)T⑨
将a1,a2,…an代入得:vn=v0-
(1+2+3+…+n)
vn=v0-
?
⑩
令vn=0,解得n=4.5,故车停前最多可以放5块.
答:(1)小车的质量10kg,车与地面间的动摩擦因数0.25.
(2)车停止对车上放有5块砖块.
放上第一块砖后车减速运动,加速度大小为a1,由图象得a1=
| △v |
| △t |
对小车由牛顿第二定律:μmg=Ma1③
由①②③式联立解得:M=10kg④
μ=0.25⑤
(2)放上第一块砖后1s,车的速度为v1,加速度为a1v1=v0-a1T⑥
a1=
| μmg |
| M |
放上第二块砖后1s车的速度为v2=v1-a2T
a2=
| 2μmg |
| M |
同理v3=v2-a3T
放上第n块砖作用1s后车速为vn,加速度为anvn=vn-1-anT⑦
an=
| nμmg |
| M |
由以上各式可得vn=v0-(a1+a2+…+an)T⑨
将a1,a2,…an代入得:vn=v0-
| μmg |
| M |
vn=v0-
| μmg |
| M |
| n(n+1) |
| 2 |
令vn=0,解得n=4.5,故车停前最多可以放5块.
答:(1)小车的质量10kg,车与地面间的动摩擦因数0.25.
(2)车停止对车上放有5块砖块.
点评:解决本题的关键知道小车所受的合力等于增加的摩擦力,会根据牛顿第二定律求出加速度的通项式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012?浠水县模拟)某电视台娱乐节目组在游乐园举行家庭做运砖块比赛活动,比赛规则是:向行驶中的小车上搬放砖块,且每次只能将一块砖无初速的放到车上,车停止时立即停止搬放,以车上砖块多少决定胜负,已知每块砖质量m=0.8kg,小车上表面光滑且足够长,比赛过程中车始终受恒定牵引力F=25N作用,未放砖块时车以v0=2.5m/s匀速前进,某家庭上场比赛时每隔t=1s搬放一块,图中仅画出了比赛开始1s内车运动的v-t图象,g=10m/s2.
(2012?浠水县模拟)某电视台娱乐节目组在游乐园举行家庭做运砖块比赛活动,比赛规则是:向行驶中的小车上搬放砖块,且每次只能将一块砖无初速的放到车上,车停止时立即停止搬放,以车上砖块多少决定胜负,已知每块砖质量m=0.8kg,小车上表面光滑且足够长,比赛过程中车始终受恒定牵引力F=25N作用,未放砖块时车以v0=2.5m/s匀速前进,某家庭上场比赛时每隔t=1s搬放一块,图中仅画出了比赛开始1s内车运动的v-t图象,g=10m/s2.
 某电视台娱乐节目组在游乐园举行家庭搬运砖块比赛活动,比赛规则是:向行驶中的小车上搬放砖块,且每次只能将一块砖无初速地放到车上,车停止时立即停止搬放,以车上砖块多少决定胜负.已知每块砖质量
某电视台娱乐节目组在游乐园举行家庭搬运砖块比赛活动,比赛规则是:向行驶中的小车上搬放砖块,且每次只能将一块砖无初速地放到车上,车停止时立即停止搬放,以车上砖块多少决定胜负.已知每块砖质量