题目内容
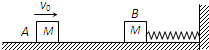如图，在光滑的水平面上，有质量均为m的A、B两个物体．B与轻弹簧一端相连，弹簧的另一端固定在墙上．开始弹簧处于原长．A以一定的速度与B发生正碰，碰撞时间极短．碰后两物体以相同的速度压缩弹簧，弹簧的最大弹性势能为Ep．不计一切摩擦．求碰撞前物体A的速度v0．分析：A、B正碰时，A、B组成的系统动量守恒，根据动量守恒可以求出两物体共同的速度为多少；a、b两物体在压缩弹簧的过程中只有弹力做功，系统满足机械能守恒条件，系统的机械能守恒，即弹簧的最大弹性势能等于系统减少的动能．
解答：解：设碰撞前A的速度为v0，A与B碰后它们共同的速度为v
以A、B为研究对象，由动量守恒定律 mv0=2mv
以A、B、弹簧为研究对象，由能量守恒得
?2mv2=Ep．
由以上两式得v0=2
答：碰撞前物体A的速度是2
．
以A、B为研究对象，由动量守恒定律 mv0=2mv
以A、B、弹簧为研究对象，由能量守恒得
| 1 |
| 2 |
由以上两式得v0=2
|
答：碰撞前物体A的速度是2
|
点评：能根据动量守恒条件判断系统动量守恒并能列式求解，能根据机械能守恒条件判断系统机械能守恒并列式求解是解决本题两问的关键．
练习册系列答案
阅读快车系列答案
相关题目
在光滑的水平面内，一质量m=1kg的质点以速度V0=10m/s沿x轴正方向运动，经过原点后受一沿y轴正方向的恒力F=15N作用，直线OA与x轴成a=37°，如图所示曲线为质点的轨迹图（g取10m/s2 sin37°=0.6 cos37°=0.8 ） 求：
如图，在光滑水平面内的弹簧振子连接一根长软绳，以平衡位置O点为原点沿绳方向取x轴．振子从O以某一初速度向A端开始运动，振动频率为f=10Hz，当振子从O点出发后，第二次返回O点时，软绳上x=15cm处的质点恰好第一次到达波峰，则下列说法正确的是（ ）
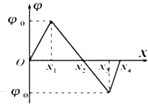在光滑的水平面内有一沿x轴的静电场，其电势φ随x坐标值的变化图线如图所示．一质量为m，带电量为q的带正电小球（可视为质点）从O点以初速度v0沿x轴正向移动．下列叙述正确的是（ ）| A、若小球能运动到x1处，则该过程小球所受电场力逐渐增大 | ||||||||
| B、带电小球从x1运动到x3的过程中，电势能先减小后增大 | ||||||||
C、若该小球能运动到x4处，则初速度v0至少为2
| ||||||||
D、若v0为2
|
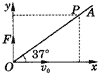在光滑的水平面内，一质量m=1kg的质点，以速度v0=10m/s沿x轴正方向运动，经过原点后受一沿y轴正方向的恒力F=5N作用，直线OA与x轴成37°角，如图所示．如果质点的运动轨迹与直线OA相交于P点，则质点从O点到P点所经历的时间为
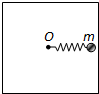如图所示，在光滑的水平面内，用轻弹簧拉住一质量为m的小球，轻弹簧的另一端固定在转轴上的O点．轻弹簧的劲度系数为k，原长为l．求小球绕O点转动的角速度分别为ω1=