题目内容
 在光滑的水平面内,一质量m=1kg的质点以速度V0=10m/s沿x轴正方向运动,经过原点后受一沿y轴正方向的恒力F=15N作用,直线OA与x轴成a=37°,如图所示曲线为质点的轨迹图(g取10m/s2 sin37°=0.6 cos37°=0.8 ) 求:
在光滑的水平面内,一质量m=1kg的质点以速度V0=10m/s沿x轴正方向运动,经过原点后受一沿y轴正方向的恒力F=15N作用,直线OA与x轴成a=37°,如图所示曲线为质点的轨迹图(g取10m/s2 sin37°=0.6 cos37°=0.8 ) 求:(1)如果质点的运动轨迹与直线OA相交于P点,质点从0点到P点所经历的时间以及P点的坐标.
(2)质点经过 P点的速度大小.
分析:将质点的运动分解为x方向和y方向,在x方向做匀速直线运动,在y方向做匀加速直线运动,结合牛顿第二定律和运动学公式进行分析求解.
解答:解:把运动分解为x方向和y方向,F并不会改变x方向速度.设经过时间t,物体到达P点
(1)xP=v0t,
yP=
?
t2,
又
=cot37°
联解得
t=1s,x=10m,y=7.5m,
则坐标(10m,7.5m)
(2)vy=
t=15m/s.
?∴v=
=5
m/s,
?tanα=
=
=
,
?∴α=arctg(
),α为v与水平方向的夹角.
答:(1)质点从0点到P点所经历的时间为1s,P点的坐标为(10m,7.5m)
(2)质点经过 P点的速度大小为5
m/s.
(1)xP=v0t,
yP=
| 1 |
| 2 |
| F |
| m |
又
| xp |
| yp |
联解得
t=1s,x=10m,y=7.5m,
则坐标(10m,7.5m)
(2)vy=
| F |
| m |
?∴v=
|
| 13 |
?tanα=
| vy |
| v0 |
| 15 |
| 10 |
| 3 |
| 2 |
?∴α=arctg(
| 3 |
| 2 |
答:(1)质点从0点到P点所经历的时间为1s,P点的坐标为(10m,7.5m)
(2)质点经过 P点的速度大小为5
| 13 |
点评:解决本题的关键对曲线运动的分解,理清分运动的规律,结合牛顿第二定律和运动学公式进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
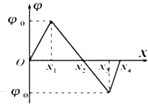 在光滑的水平面内有一沿x轴的静电场,其电势φ随x坐标值的变化图线如图所示.一质量为m,带电量为q的带正电小球(可视为质点)从O点以初速度v0沿x轴正向移动.下列叙述正确的是( )
在光滑的水平面内有一沿x轴的静电场,其电势φ随x坐标值的变化图线如图所示.一质量为m,带电量为q的带正电小球(可视为质点)从O点以初速度v0沿x轴正向移动.下列叙述正确的是( )| A、若小球能运动到x1处,则该过程小球所受电场力逐渐增大 | ||||||||
| B、带电小球从x1运动到x3的过程中,电势能先减小后增大 | ||||||||
C、若该小球能运动到x4处,则初速度v0至少为2
| ||||||||
D、若v0为2
|
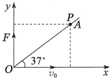 在光滑的水平面内,一质量m=lkg的质点以速度v0=10m/s沿x轴正方向运动,经过原点后受一沿y轴正方向的恒力F=5N作用,直线OA与x轴成37°角,如图所示,(sin37°=0.6,cos37°=0.8)
在光滑的水平面内,一质量m=lkg的质点以速度v0=10m/s沿x轴正方向运动,经过原点后受一沿y轴正方向的恒力F=5N作用,直线OA与x轴成37°角,如图所示,(sin37°=0.6,cos37°=0.8)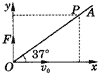 在光滑的水平面内,一质量m=1kg的质点,以速度v0=10m/s沿x轴正方向运动,经过原点后受一沿y轴正方向的恒力F=5N作用,直线OA与x轴成37°角,如图所示.如果质点的运动轨迹与直线OA相交于P点,则质点从O点到P点所经历的时间为
在光滑的水平面内,一质量m=1kg的质点,以速度v0=10m/s沿x轴正方向运动,经过原点后受一沿y轴正方向的恒力F=5N作用,直线OA与x轴成37°角,如图所示.如果质点的运动轨迹与直线OA相交于P点,则质点从O点到P点所经历的时间为 在光滑的水平面内有一沿x轴的静电场,其电势Ф随x坐标值的变化图线如图所示.一质量为m,带电量为q的带正电小球(可视为质点)从O点以初速度v0沿x轴正向移动.下列叙述正确的是( )
在光滑的水平面内有一沿x轴的静电场,其电势Ф随x坐标值的变化图线如图所示.一质量为m,带电量为q的带正电小球(可视为质点)从O点以初速度v0沿x轴正向移动.下列叙述正确的是( )