题目内容
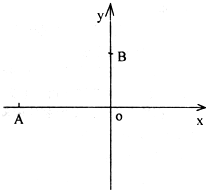如图所示，在xoy平面内有垂直坐标平面的范围足够大的匀强磁场，磁感强度为B，一带正电荷、电量为Q、质量为m的粒子，从坐标原点．以某一初速度垂直射入磁场，其轨迹与x、y轴的交点A、B到O点的距离分别为a、b，试求：（1）粒子初速度方向与x轴夹角θ
（2）粒子初速度的大小．
分析：（1）粒子进入磁场后做匀速圆周运动，作出运动轨迹，由几何关系即可求解；
（2）根据几何关系求出半径R，根据洛伦兹力提供向心力公式即可求解．
（2）根据几何关系求出半径R，根据洛伦兹力提供向心力公式即可求解．
解答：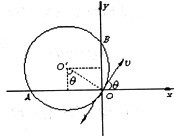
解：（1）磁场方向垂直坐标平面向里时，粒子初速度方向与x轴的夹角为θ，射入磁场做匀速圆周运动，由几何关系可作出轨迹如图所示：
设圆半径为R，由数学关系得：
=Rsinθ①
=Rcosθ②
由①②解得：tanθ=
所以θ=arctan
当磁场方向垂直坐标平面向外时，粒子初速度方向与x轴夹角为π+θ=π+arctan
（2）由①②解得：R=
由洛伦兹力提供向心力得：
BQv=m
解得：v=
答：（1）粒子初速度方向与x轴夹角θ为arctan
或π+arctan
；
（2）粒子初速度的大小为
．
解：（1）磁场方向垂直坐标平面向里时，粒子初速度方向与x轴的夹角为θ，射入磁场做匀速圆周运动，由几何关系可作出轨迹如图所示：设圆半径为R，由数学关系得：
| a |
| 2 |
| b |
| 2 |
由①②解得：tanθ=
| a |
| b |
所以θ=arctan
| a |
| b |
当磁场方向垂直坐标平面向外时，粒子初速度方向与x轴夹角为π+θ=π+arctan
| a |
| b |
（2）由①②解得：R=
| ||
| 2 |
由洛伦兹力提供向心力得：
BQv=m
| v2 |
| R |
解得：v=
QB
| ||
| 2m |
答：（1）粒子初速度方向与x轴夹角θ为arctan
| a |
| b |
| a |
| b |
（2）粒子初速度的大小为
QB
| ||
| 2m |
点评：本题主要考查了带电粒子在磁场中的运动问题，要求同学们能画出粒子运动轨迹，结合几何关系求解，难度适中．
练习册系列答案
阅读快车系列答案
相关题目
（2013?安徽模拟）如图所示，在xoy平面上，直线OM与x轴正方向夹角为45°，直线OM左侧存在平行y轴的匀强电场，方向沿y轴负方向．直线OM右侧存在垂直xoy平面向里的磁感应强度为B的匀强磁场．一带电量为q质量为m带正电的粒子（忽略重力）从原点O沿x轴正方向以速度vo射入磁场．此后，粒子穿过磁场与电场的边界三次，恰好从电场中回到原点O．（粒子通过边界时，其运动不受边界的影响）试求：
如图所示，在xOy平面的y轴左侧存在沿y轴正方向的匀强电场，y轴右侧区域Ⅰ内存在磁感应强度大小B1=
（2006?连云港二模）如图所示，在xoy平面上，一个以原点O为中心、半径为R的圆形区域内存在着一匀强磁场．磁场的磁感应强度为B，方向垂直于xoy平面向里．在O点处原来静止着一个具有放射性的原子核--氮（
如图所示，在xOy平面上，一个以原点O为圆心，半径为4R的原型磁场区域内存在着匀强磁场，磁场的方向垂直于纸面向里，在坐标（-2R，0）的A处静止着一个具有放射性的原子核氮713N．某时刻该核发生衰变，放出一个正电子和一个反冲核，已知正电子从A处射出时速度方向垂直于x轴，且后来通过了y轴，而反冲核刚好不离开磁场区域．不计重力影响和离子间的相互作用．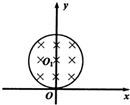
如图所示，在xOy平面上，以y轴上点Ol为圆心，半径为R=0.3m的圆形区域内，分布着一个方向垂直于xOy平面向里，磁感应强度大小为B=0.5T的匀强磁场．一个比荷