Question

滑雪者从A点由静止沿斜面滑下，经一平台后水平飞离B点，地面上紧靠平台有一个水平台阶，空间几何尺度如图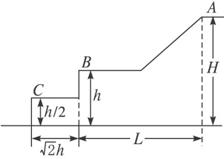6-4-6所示.斜面、平台与滑雪板之间的动摩擦因数为μ，假设滑雪者由斜面底端进入平台后，立即沿水平方向运动，且速度大小不变.求：

图6-4-6

(1)滑雪者离开B点时的速度大小;

(2)滑雪者从B点开始做平抛运动的水平距离s.

Answer 1

解析：滑雪者从A点运动到B点的过程中，由于滑雪者与平台及斜面之间存在摩擦，所以应用动能定理便可解得滑雪者到达B点时的速度；从B点开始，滑雪者开始做平抛运动，有可能运动到平台，也有可能直接运动到地面上，因此对滑雪者的运动情况应分两种情况进行讨论.

(1)设滑雪者质量为m，斜面与水平面夹角为θ，滑雪者滑行过程中克服摩擦力做功W_F=μmgcosθ·s+μmg(L-scosθ)=μmgL.由动能定理得：mg(H-h)-μmgL=mv²

离开B点时的速度为：v=

（2）设滑雪者离开B点后落在台阶上，=gt₁²  s₁=vt₁＜h

可解得s₁=，此时必须满足H-μL＜2h

当H-μL＞2h时，滑雪者直接落到地面上，h=gt₂²  s₂=vt₂

可解得s₂=.

答案： (1)   (2)s=或s=