Question

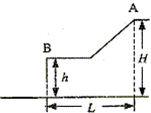
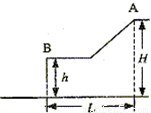
B． 滑雪者从A点由静止沿斜面滑下，沿一平台滑过后水平飞离B点，最后落到地面，空间几何尺度（H、h和L）如图所示．斜面、平台与滑雪板之间的动摩擦因数为μ．假设滑雪者由斜面底端进入平台后立即沿水平方向运动，且速度大小不变．求：
（1）滑雪者从A到B的过程中，克服摩擦力做的功；
（2）滑雪者离开B点时的速度大小；
（3）滑雪者从B点开始做平抛运动，到达地面时的速度大小．

Answer 1

分析：（1）滑雪者从A到B的过程中，求出摩擦力，由功的公式求解克服摩擦力做的功；
（2）根据动能定理研究A到B的过程，求出滑雪者离开B点时的速度大小；
（3）滑雪者离开B点到着地过程，只有重力做功，机械能守恒，即可滑雪者求得到达地面时的速度大小．

解答：解：
（1）设滑雪者质量为m，斜面长为s，斜面与水平面夹角为θ，滑雪者滑行过程中克服摩擦力做功：
    W=μmgcosθ?s+μmg（L-scosθ）=μmgL 　　　　    
（2）A到B的过程，由动能定理得
    mg（H-h）-μmgL=

1

2

mv2
故滑雪者离开B点时的速度为 v=

2g(H-h-μL)

               
（3）滑雪者离开B点到着地过程，机械能守恒，则有：
  

1

2

mv2+mgh=

1

2

mv′2
解得着地速度v′=

2g(H-μL)

答：
（1）滑雪者从A到B的过程中，克服摩擦力做的功是μmgL；
（2）滑雪者离开B点时的速度大小是

2g(H-h-μL)

；
（3）滑雪者从B点开始做平抛运动，到达地面时的速度大小是

2g(H-μL)

．

点评：动能定理的应用要选取合适的研究过程，其中对于总功的求解是易错点．从本题看出，滑动摩擦力做功W=μmgL，与水平位移大小L成正比．