题目内容
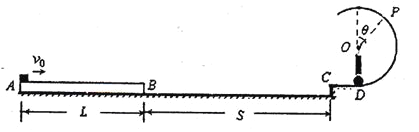
【题目】图所示,一长L=4.5m、质量m1=1kg的长木板静止在水平面上,与地面间的动摩擦因数μ1=0.1.长木板B端距光滑水平轨道CD的C端距离S=7m,长木板的上表面与CD面等高.一小滑块以v0=9m/s的初速度滑上长木板的A端后长木板开始运动.小滑块质量m2=2kg,与长木板之间的动摩擦因数μ2=0.4,长木板运动到C处时即被半圆粘连.水平轨道CD右侧有一竖直光滑圆形轨道在D点与水平轨道平滑连接,圆心为O,半径R=0.4m.一轻质弹簧一端固定在O点的轴上,一端拴着一个质量与小滑块相等的小球,弹簧的原长为l0=0.5m,劲度系数k=100N/m,不计小滑块和小球的大小,取重力加速度的大小g=10m/s2.求:
(1)小滑块刚滑上长木板时,长木板的加速度大小a1和小滑块的加速度大小a2;
(2)长木板与水平轨道C端发生粘连前瞬间的速度vt;
(3)小滑块与小球在D点发生弹性碰撞后,小球随即沿圆弧轨道运动,通过分析可知小球到达P点时离开圆轨道,求P、O连线与竖直方向夹角θ的余弦值.
【答案】(1)5m/s2 4m/s2 (2)4m/s; (3)余弦值为![]()
【解析】(1)由题意知滑块带动长木板滑动,先以滑块为研究对象,长木板对滑块的摩擦力使滑块产生加速度,故有:
μ2m2g=m2a2
可得滑块的加速度为:
![]()
长木板在滑块和地面滑动摩擦力共同作用下产生加速度有:
![]() ;
;
(2) 设滑块和木板达到共同速度v1时间为t
则v1=a1t
v1=v0﹣a2t代入数据解得
![]()
v1=5×1m/s=5m/s此过程中长木板的位移为:
![]()
小滑块的位移为:
![]()
滑块与木板的位移差为:△x=x2﹣x1=7﹣2.5m=4.5m
因为△x=L,所以滑块刚好滑至长木板的右端时,两者具有共同的速度,经后长木板与滑块一起做匀减速运动
加速度为:
![]()
因为|a3|<|a2|,所以滑块和长木板一起减速,设滑行到C处的速度为vC,
根据速度位移关系有:
![]()
即长木板与水平轨道C端发生粘连前瞬间的速度vt为4m/s;
(3) 小滑块和小球质量相同,在D处弹性碰撞后,两球交换速度,小球以vC=4m/s沿圆弧轨道向上运动,
设小球离开轨道时的速度为v
由机械能守恒有:
![]()
根据牛顿第二定律有:
![]()
由以上两式解得:![]() 。
。








