题目内容
8. 如图所示,质量为M的木板上放着一质量为m的木块,木块与木板间的动摩擦因数为μ1,木板与水平地面间动摩擦因数为μ2.
如图所示,质量为M的木板上放着一质量为m的木块,木块与木板间的动摩擦因数为μ1,木板与水平地面间动摩擦因数为μ2.(1)若在M上加一水平外力F,当F为多大时,m与M一起匀速运动;
(2)若在m上加一水平外力F,使m与M能一起匀速运动,则μ1与μ2应满足什么条件;
(3)若在M上加一水平外力F,使M能从m下抽出,则F至少为多大.
分析 (1)在M上加一水平外力F,木块匀速运动,受力平衡,则水平方向不受力,木板匀速运动,受力平衡,拉力等于滑动摩擦力;
(2)在m上加一水平外力F,m与M能一起匀速运动,则拉力小于木块的最大静摩擦力,对整体受力分析,则拉力等于地面对木板的滑动摩擦力,据此列式求解;
(3)对m和M分别进行受力分析,求出合外力的表达式,根据牛顿第二定律求出加速度的表达式,能将木板抽出来的条件是木板的加速度要大于木块的加速度.
解答 解:(1)在M上加一水平外力F,木块匀速运动,受力平衡,则水平方向不受力,
木板匀速运动,受力平衡,竖直方向FN=(m+M)g,
水平方向F=f=μ2FN=μ2(m+M)g
(2)在m上加一水平外力F,m与M能一起匀速运动,
对木块m受力分析,水平方向受拉力F和静摩擦力,则F<μ1mg①,
对整体受力分析,水平方向有F=μ2(M+m)g②
由①②解得:${μ}_{2}<\frac{m}{m+M}{μ}_{1}$
(3)对m与M分别进行受力分析如图所示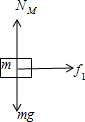
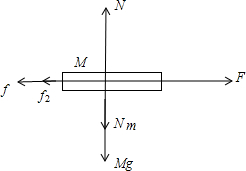
对m有:
f1=ma1 ③
f1=μ1NM=μ1mg ④
由③④得:
a1=μ1g
对M进行受力分析有:
F-f-f2=M•a2 ⑤
f1和f2互为作用力与反作用力故有:
f1=f2=μ1•mg ⑥
f=μ2(M+m)•g ⑦
由⑤⑥⑦可得
a2=$\frac{F-({μ}_{1}+{μ}_{2})mg}{M}-{μ}_{2}g$
要将木板从木块下抽出,必须使a2>a1
即:$\frac{F-({μ}_{1}+{μ}_{2})mg}{M}-{μ}_{2}g$>μ1g
解得:F>[(μ1+μ2)(M+m)]g
答:(1)若在M上加一水平外力F,当F为μ2(m+M)g时,m与M一起匀速运动;
(2)若在m上加一水平外力F,使m与M能一起匀速运动,则μ1与μ2应满足${μ}_{2}<\frac{m}{m+M}{μ}_{1}$;
(3)若在M上加一水平外力F,使M能从m下抽出,则F至少[(μ1+μ2)(M+m)]g.
点评 正确的受力分析,能根据平衡条件列式是解题的关键,知道能将木板从木块下抽出的条件是木板产生的加速度比木块产生的加速度来得大,难度适中.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案| A. | 电场中电场线一定是直线 | |
| B. | 电势差的大小与零电势点的选取有关 | |
| C. | 电场中电势高的地方电势能越高 | |
| D. | 电场线方向与等势面处处相垂直 |
 如图所示,物体质量为1kg,斜向上的拉力F=10N,物体和水平面间的动摩擦因数μ=0.5,物体在F的作用下由静止开始运动10s,则在这段时间内拉力F对物体做功为2400J (g取10m/s2).
如图所示,物体质量为1kg,斜向上的拉力F=10N,物体和水平面间的动摩擦因数μ=0.5,物体在F的作用下由静止开始运动10s,则在这段时间内拉力F对物体做功为2400J (g取10m/s2). 
| A. | 锁舌D与锁槽E之间的正压力的大小为$\frac{\sqrt{2}kx}{1-2μ-{μ}^{2}}$ | |
| B. | 锁舌D与锁槽E之间的正压力的大小$\frac{kx}{1-2{μ}^{2}}$ | |
| C. | 出现自锁现象的最小摩擦因数为μ=0.414 | |
| D. | 出现自锁现象的最小摩擦因数为μ=0.207 |

| A. | S闭合时通过R1与R2的电流之比为2:1 | |
| B. | S断开时,R1与R2的功率之比为1:10 | |
| C. | S断开与闭合两情况下,电阻R1两端的电压之比为7:12 | |
| D. | S断开与闭合两情况下,电阻R2的功率之比为7:12 |
 如图所示的曲线表示某一电场的电场线(未表明方向),把一带电荷量为2×10-8C的正点电荷从A点移至B点时,电场力做了6×10-4J的功,且在B点受到电场力为4×10-6N,试求:
如图所示的曲线表示某一电场的电场线(未表明方向),把一带电荷量为2×10-8C的正点电荷从A点移至B点时,电场力做了6×10-4J的功,且在B点受到电场力为4×10-6N,试求: 如图所示,某物块(可看成质点)质量为m=0.1kg从A点沿竖直光滑的$\frac{1}{4}$圆弧轨道,由静止开始滑下,圆弧轨道的半径R=0.2m,末端B点与水平传送带相切,物块由B点滑上粗糙的传送带.传送带BC之间长度L=1.5m,若传送带静止,物块滑到传送带的末端C点后做平抛运动,落到水平地面上的D点,已知C点到地面的高度H=5m,C点到D点的水平距离为x1=1m,g=10m/s2.求:
如图所示,某物块(可看成质点)质量为m=0.1kg从A点沿竖直光滑的$\frac{1}{4}$圆弧轨道,由静止开始滑下,圆弧轨道的半径R=0.2m,末端B点与水平传送带相切,物块由B点滑上粗糙的传送带.传送带BC之间长度L=1.5m,若传送带静止,物块滑到传送带的末端C点后做平抛运动,落到水平地面上的D点,已知C点到地面的高度H=5m,C点到D点的水平距离为x1=1m,g=10m/s2.求: 某同学把附有滑轮的长木板放在实验桌上,将细绳一端拴在小车上,另一端绕过定滑轮,挂上适当的钩码,使小车在钩码的牵引下运动,以此定量探究绳拉力做功与小车动能变化的关系,此外还准备了打点计时器及配套的电源、导线、复写纸、纸带、小木块等.组装的实验装置如图所示.
某同学把附有滑轮的长木板放在实验桌上,将细绳一端拴在小车上,另一端绕过定滑轮,挂上适当的钩码,使小车在钩码的牵引下运动,以此定量探究绳拉力做功与小车动能变化的关系,此外还准备了打点计时器及配套的电源、导线、复写纸、纸带、小木块等.组装的实验装置如图所示.