题目内容
7.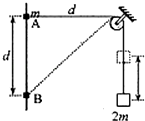 如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d.杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )
如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d.杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )| A. | 环到达B处时,重物上升的高度h=($\sqrt{2}$-1)d | |
| B. | 环到达B处时,环与重物的速度大小相等 | |
| C. | 环从A到B,环减少的机械能等于重物增加的机械能 | |
| D. | 环能下降的最大高度为$\frac{4}{3}$d |
分析 环刚开始释放时,重物由静止开始加速.根据数学几何关系求出环到达B处时,重物上升的高度.对B的速度沿绳子方向和垂直于绳子方向分解,在沿绳子方向上的分速度等于重物的速度,从而求出环在B处速度与重物的速度之比.环和重物组成的系统机械能是守恒的.
解答 解:A、根据几何关系有,环从A下滑至B点时,下降的高度为 d,则重物上升的高度h=$\sqrt{2}$d-d=($\sqrt{2}$-1)d,故A正确;
B、环到达B处时,对环B的速度沿绳子方向和垂直于绳子方向分解,在沿绳子方向上的分速度等于重物的速度,有:v环cos45°=v物,所以有v环=$\sqrt{2}$v物,故B错误;
C、环下滑过程中无摩擦力做功,故系统机械能守恒,即有环减小的机械能等于重物增加的机械能,故C正确;
D、设环下滑到最大高度为h时环和重物的速度均为0,此时重物上升的最大高度为$\sqrt{{h}^{2}+{d}^{2}}$-d,根据系统的机械能守恒有:mgh=2mg($\sqrt{{h}^{2}{+d}^{2}}$-d)
解得:h=$\frac{4}{3}$d,故D正确.
故选:ACD.
点评 解决本题的关键知道系统机械能守恒,知道环沿绳子方向的分速度的等于重物的速度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.电容器A的电容比电容器B的电容大,这表明( )
| A. | A所带的电荷量比B多 | |
| B. | A比B能容纳更多的电荷 | |
| C. | A的体积比B的体积大 | |
| D. | 两电容器的电压都改变1V时,A的电荷量改变比B的大 |
15. 匝数为100的线圈的面积S=100cm2,放在方向如图所示的匀强磁场中.线圈平面与磁场的方向垂直,当磁感应强度由2×10-3经过5s钟均匀减小到0时,感应电动势的大小为( )
匝数为100的线圈的面积S=100cm2,放在方向如图所示的匀强磁场中.线圈平面与磁场的方向垂直,当磁感应强度由2×10-3经过5s钟均匀减小到0时,感应电动势的大小为( )
 匝数为100的线圈的面积S=100cm2,放在方向如图所示的匀强磁场中.线圈平面与磁场的方向垂直,当磁感应强度由2×10-3经过5s钟均匀减小到0时,感应电动势的大小为( )
匝数为100的线圈的面积S=100cm2,放在方向如图所示的匀强磁场中.线圈平面与磁场的方向垂直,当磁感应强度由2×10-3经过5s钟均匀减小到0时,感应电动势的大小为( )| A. | 4×10-4V | B. | 2×10-3V | C. | 4×10-2V | D. | 0.2V |
2.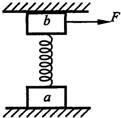 如图所示,质量均为m的a、b两物体,放在两固定的水平挡板之间,物体间用一竖直放置的轻弹簧连接,在b物体上施加水平拉力F后,两物体始终保持静止状态,已知重力加速度为g,则下列说法正确的是( )
如图所示,质量均为m的a、b两物体,放在两固定的水平挡板之间,物体间用一竖直放置的轻弹簧连接,在b物体上施加水平拉力F后,两物体始终保持静止状态,已知重力加速度为g,则下列说法正确的是( )
 如图所示,质量均为m的a、b两物体,放在两固定的水平挡板之间,物体间用一竖直放置的轻弹簧连接,在b物体上施加水平拉力F后,两物体始终保持静止状态,已知重力加速度为g,则下列说法正确的是( )
如图所示,质量均为m的a、b两物体,放在两固定的水平挡板之间,物体间用一竖直放置的轻弹簧连接,在b物体上施加水平拉力F后,两物体始终保持静止状态,已知重力加速度为g,则下列说法正确的是( )| A. | a物体对水平面的压力大小一定大于2mg | |
| B. | a物体所受摩擦力的大小为0 | |
| C. | b物体所受摩擦力的大小为F | |
| D. | 弹簧对b物体的弹力大小可能等于mg |
12.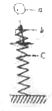 如图所示,小球自a点静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中(选地面为零势位)( )
如图所示,小球自a点静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中(选地面为零势位)( )
 如图所示,小球自a点静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中(选地面为零势位)( )
如图所示,小球自a点静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中(选地面为零势位)( )| A. | 小球机械能守恒 | |
| B. | 小球的重力势能随时间均匀减少 | |
| C. | 小球在b点时动能最大 | |
| D. | a到c点整个过程,小球重力势能的减小量等于弹簧弹性势能的增加量 |
17.下列几种表述中,涉及到的计时数据,指时间间隔的是( )
| A. | 中央电视台新闻联播节目用时30分钟 | |
| B. | 1997年7月1日零时中国对香港恢复行使主权 | |
| C. | 2007年10月24日18时5分5秒嫦娥一号在西昌卫星发射中心升空 | |
| D. | 北京奥运会开幕式于2008年8月8日晚8时开始 |
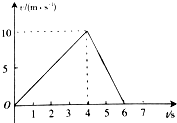 一物体做直线运动的速度-时间图象如图所示,根据图象求物体第6s末相对于起点的位移是30m,物体第2s末的加速度是2.5m/s2,物体第5s末的加速度大小是5m/s2.
一物体做直线运动的速度-时间图象如图所示,根据图象求物体第6s末相对于起点的位移是30m,物体第2s末的加速度是2.5m/s2,物体第5s末的加速度大小是5m/s2.