��Ŀ����
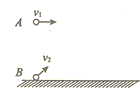
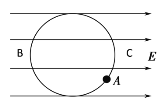
����Ŀ����ͼ��ʾ������ֱƽ������һˮƽ���ҵ���ǿ�糡����ǿE��1.0��104 N/C���뾶R��2.0m�Ĺ⻬��ԵϸԲ���ι����ֱ�����ҹ̶�����һ����m��0.4 kg�������q����3.0��10��4 C�Ĵ���С��ϸԲ���ι����ֹ��λ��A���ֶ�С�������߷�������һ˲ʱ�ٶ�![]() ��ʹС��ǡ�����ڹ⻬��ԵϸԲ���ι������Բ���˶���ȡԲ������͵�Ϊ�������ܺ͵����ܵ������ܵ㣮��֪BC��Բ���ι����һ��ˮƽֱ����g��10m/s2��sin370��0.6��cos370��0.8������˵����ȷ���ǣ�
��ʹС��ǡ�����ڹ⻬��ԵϸԲ���ι������Բ���˶���ȡԲ������͵�Ϊ�������ܺ͵����ܵ������ܵ㣮��֪BC��Բ���ι����һ��ˮƽֱ����g��10m/s2��sin370��0.6��cos370��0.8������˵����ȷ���ǣ�
A. ��λ��A��ֹʱԲ����С��ĵ�����СΪ5N
B. ˲ʱ�ٶ�![]() �Ĵ�СΪ
�Ĵ�СΪ![]()
C. ˲ʱ�ٶ�![]() �Ĵ�СΪ
�Ĵ�СΪ![]()
D. С��ͨ��B��ʱ�Ļ�е����С
���𰸡�ACD
��������
A. С����A������ƽ�⣬���ݹ�����ƽ���,����N=![]() N=5N.��A��ȷ��
N=5N.��A��ȷ��
B. ��糡���������ĺ�����������ֱ����ļн�Ϊ�ȣ���tan��=![]() ������=37.�ڵ�Ч��ߵ㣬��С�ٶ�Ϊ�㣬���ݶ��ܶ�����,F2R=0
������=37.�ڵ�Ч��ߵ㣬��С�ٶ�Ϊ�㣬���ݶ��ܶ�����,F2R=0![]() ��
��
�������ݽ��vA=10m/s.��B����C��ȷ��
D. ��A��B�Ĺ����У��糡�������ĸ�����࣬���е����ʧ��࣬��֪С��ͨ��B��ʱ�Ļ�е����С����D��ȷ��
��ѡ��ACD.

 ��У����ϵ�д�
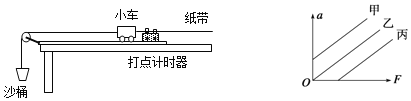
��У����ϵ�д�����Ŀ��������̽�����ٶ������������Ĺ�ϵ����ʵ��ʱ���������ֽ���ļ��ٶȺ���õķ�ӳ���ٶ�a����F�Ĺ�ϵ���й����ϼ�¼�ڱ�1�У�����õķ�ӳ���ٶ�a������M�Ĺ�ϵ���������ڱ�2��
��1
a/��ms��2�� | 1.98 | 4.06 | 5.95 | 8.12 |
F/N | 1.00 | 2.00 | 3.00 | 4.00 |
��2
a/��ms��2�� | 2.04 | 2.66 | 3.23 | 3.98 |
| 0.50 | 0.67 | 0.80 | 1.00 |
����ͼ���������ݣ��ֱ���a��F��a��![]() ͼ��
ͼ��

��1����ͼ������ж�����Mһ��ʱ��a��F�Ĺ�ϵΪ_____����Fһ��ʱ��a��M�Ĺ�ϵΪ_____����������������
��2����a��Fͼ���֪M��_____kg��
��3����![]() ͼ���֪F��_____N��
ͼ���֪F��_____N��