题目内容
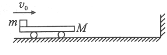
【题目】如图所示,一质量M=2kg、长L=1m的小车静止在光滑的水平地面上,有一质量m=1 kg的物块(可视为质点)以水平向右、大小为v0=3 m/s的初速度从左端滑上小车,当物块滑到小车的中点时刚好相对于小车静止.以后两者一起向右运动,当小车与竖直墙壁发生碰撞后立即以原速率返回.试求:(g取10 m/s2)
(1)物块与小车相对静止时的速度v;
(2)物块与小车间的动摩擦因数![]() ;
;
(3)物块在运动的过程中离竖直墙壁的最小距离d.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】
(1)根据“地面光滑,物块在木板上相对滑动的过程”可知,本小问考查板块模型的运动问题,根据系统的动量守恒列式计算共同的速度;(2)根据“小车的中点时刚好相对于小车静止”可知,本题考查摩擦生热,根据功能关系,运用相对位移列式求解动摩擦因数![]() ;(3)根据“物块运动的最小距离d”可知,本小问考查动力学问题,根据牛顿第二定律和运动学的位移公式求解.
;(3)根据“物块运动的最小距离d”可知,本小问考查动力学问题,根据牛顿第二定律和运动学的位移公式求解.
(1)因为地面光滑,所以小车和物块组成的系统动量守恒,取水平向右为正方向,由动量守恒定律得:mv0=(M+m)v
解得: ![]()
(2)对系统,由能量守恒有:![]()
代入数据得:μ=0.6
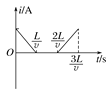
(3)当小车与墙相撞时,物块到墙的距离为:![]()
由于小车与墙碰撞时间极短且碰撞中无动能损失,可认为小车碰墙后,立即以原速率返回,而在这极短时间内,物块所受冲量可忽略,故物块速度未变,仍以v向右,当其速度减小为零时离墙最近.
该过程中物块的加速度大小为:![]()
所以在该过程中物块向右运动,有:![]()
所以物块离墙壁的最小距离为:![]()

练习册系列答案
相关题目