题目内容
(1)月球绕地球公转周期为T,月地距离为r,引力常量为G,地球质量为M,则r3与T2的比为k,k=
.
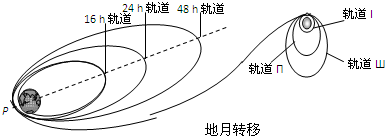
(2)一探月卫星在地月转移轨道上运行,计划通过地心和月心连线上特别位置,卫星在此处所受地球引力与月球引力的大小恰好相等.已知地球与月球的质量之比约为81:1,则该处到地心与到月心的距离之比约为
| GM |
| 4π2 |
| GM |
| 4π2 |
(2)一探月卫星在地月转移轨道上运行,计划通过地心和月心连线上特别位置,卫星在此处所受地球引力与月球引力的大小恰好相等.已知地球与月球的质量之比约为81:1,则该处到地心与到月心的距离之比约为
9:1
9:1
.分析:(1)月球绕地球公转,根据万有引力提供向心力列式求解即可;
(2)卫星所受地球引力与月球引力的大小恰好相等,根据万有引力定律列方程求解即可.
(2)卫星所受地球引力与月球引力的大小恰好相等,根据万有引力定律列方程求解即可.
解答:解:(1)月球绕地球公转周期为T,月地距离为r,引力常量为G,地球质量为M,根据万有引力提供向心力,有:
G
=mr(
)2
解得:
=
故k=
(2)卫星所受地球引力与月球引力的大小恰好相等,根据万有引力定律,有:
G
=G
解得:
=
=9
故答案为:(1)
;(2)9:1.
G
| mM |
| r2 |
| 2π |
| T |
解得:
| r3 |
| T2 |
| GM |
| 4π2 |
故k=
| GM |
| 4π2 |
(2)卫星所受地球引力与月球引力的大小恰好相等,根据万有引力定律,有:
G
| m0M | ||
|
| m0m | ||
|
解得:
| r2 |
| r1 |
|
故答案为:(1)
| GM |
| 4π2 |
点评:本题第一问关键是明确月球公转的向心力来源,第二问关键是运用万有引力定律公式列方程求解.

练习册系列答案
相关题目