题目内容
16.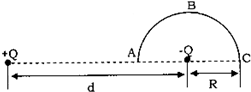 对于真空中电荷量为q的静止点电荷而言,当选取离点电荷无穷远的电势为零时,离点电荷距离为r的位置的电势为φ=$\frac{kq}{r}$(k为静电力常量),如图所示,两电荷量大小均为Q的异种点电荷相距为d,现将一质子(电荷量为+e)从两电荷连线上的A点沿以负电荷为圆心、半径为R的半圆形轨迹ABC移到C点,在质子从A到C的过程中,系统电势能的变化情况为( )
对于真空中电荷量为q的静止点电荷而言,当选取离点电荷无穷远的电势为零时,离点电荷距离为r的位置的电势为φ=$\frac{kq}{r}$(k为静电力常量),如图所示,两电荷量大小均为Q的异种点电荷相距为d,现将一质子(电荷量为+e)从两电荷连线上的A点沿以负电荷为圆心、半径为R的半圆形轨迹ABC移到C点,在质子从A到C的过程中,系统电势能的变化情况为( )| A. | 减少$\frac{2k{Q}_{e}}{{d}^{2}-{R}^{2}}$ | B. | 增加$\frac{2k{Q}_{e}R}{{d}^{2}+{R}^{2}}$ | ||
| C. | 减少$\frac{2k{Q}_{e}R}{{d}^{2}-{R}^{2}}$ | D. | 增加$\frac{2k{Q}_{e}}{{d}^{2}+{R}^{2}}$ |
分析 根据题中信息φ=$\frac{kq}{r}$公式,分别求出质子在A点和C点的电势,由公式Ep=qφ求解电势能及其变化量
解答 解:A点的电势为 φA=-k$\frac{Q}{R}$+k$\frac{Q}{d-R}$=-$\frac{kQ(d-2R)}{R(d-R)}$;C点的电势为φC=-k$\frac{Q}{R}$+k$\frac{Q}{d+R}$=-$\frac{kQd}{R(d+R)}$
则A、C间的电势差为 UAC=φA-φC=-$\frac{kQ(d-2R)}{R(d-R)}$-(-$\frac{kQd}{R(d+R)}$)=$\frac{2kQR}{{d}^{2}-{R}^{2}}$,
质子从A移到C,电场力做功为 WAC=eUAC=$\frac{2kQeR}{{d}^{2}-{R}^{2}}$,是正功,所以质子的电势能减少$\frac{2kQeR}{{d}^{2}-{R}^{2}}$,故C正确.
故选:C
点评 本题是信息给予题,关键要读懂题意,知道如何求解电势,并掌握电场力做功公式和电场力做功与电势能变化的关系

练习册系列答案
相关题目
19.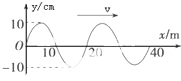 在坐标原点的波源产生一列沿x轴正方向传播的简谐横波,波速v=200m/s,已知t=0时,波刚好传播到x=40m处,如图所示.在x=400m处有一接收器(图中未画出),则下列说法正确的是( )
在坐标原点的波源产生一列沿x轴正方向传播的简谐横波,波速v=200m/s,已知t=0时,波刚好传播到x=40m处,如图所示.在x=400m处有一接收器(图中未画出),则下列说法正确的是( )
 在坐标原点的波源产生一列沿x轴正方向传播的简谐横波,波速v=200m/s,已知t=0时,波刚好传播到x=40m处,如图所示.在x=400m处有一接收器(图中未画出),则下列说法正确的是( )
在坐标原点的波源产生一列沿x轴正方向传播的简谐横波,波速v=200m/s,已知t=0时,波刚好传播到x=40m处,如图所示.在x=400m处有一接收器(图中未画出),则下列说法正确的是( )| A. | 波源开始振动时方向沿y轴正方向 | |
| B. | 从t=0开始经0.15s,x=40m的质点运动的路程为0.6m | |
| C. | 接收器在t=2s时才能接收到此波 | |
| D. | 当波刚刚传到接收器时,x=20m的质点速度刚好为0 |
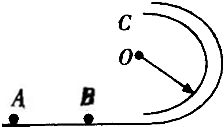 如图所示,半径为R、内径很小的光滑半圆管竖直放置,两个质量均为m的小球A、B以不同的速率进入管内,B通过最高点C时,对管壁下部的压力为0.75mg,A、B两球落地点间的距离为3R,求A通过最高点C时对管壁上部的压力.
如图所示,半径为R、内径很小的光滑半圆管竖直放置,两个质量均为m的小球A、B以不同的速率进入管内,B通过最高点C时,对管壁下部的压力为0.75mg,A、B两球落地点间的距离为3R,求A通过最高点C时对管壁上部的压力. 如图所示,固定的圆弧轨道与水平面平滑连接,轨道与水平面均光滑,质量为m的物块B与轻质弹簧栓接静止在水平面上,弹簧右端固定,质量为3m的物块A从圆弧轨道上距离水平面高h处由静止释放,与B碰撞后推着B一起运动但与B不粘连.求:
如图所示,固定的圆弧轨道与水平面平滑连接,轨道与水平面均光滑,质量为m的物块B与轻质弹簧栓接静止在水平面上,弹簧右端固定,质量为3m的物块A从圆弧轨道上距离水平面高h处由静止释放,与B碰撞后推着B一起运动但与B不粘连.求: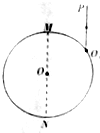 如图所示的圆表示一圆柱形玻璃砖的截面,O为其圆心,MN为直径.一束平行于MN的光线沿PO1方向从O1点射入玻璃砖,在玻璃砖内传到N点,已知PO1与MN之间的距离为$\frac{\sqrt{3}}{2}$R(R为玻璃砖的半径),真空中的光速为c,求:
如图所示的圆表示一圆柱形玻璃砖的截面,O为其圆心,MN为直径.一束平行于MN的光线沿PO1方向从O1点射入玻璃砖,在玻璃砖内传到N点,已知PO1与MN之间的距离为$\frac{\sqrt{3}}{2}$R(R为玻璃砖的半径),真空中的光速为c,求: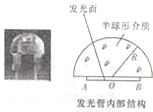 与小白炽灯泡和氖灯相比,发光二极管具有工作电压低(有的仅一点几伏),工作电流很小(有的仅零点几毫安即可发光)、抗冲击和抗震性能好、可靠性高、寿命长、通过调节电流可以方便地调节发光的强弱等特点,被广泛应用于电子显示屏和新型照明光源等领域,通常发光二极管的成品是将发光二极管的管芯封装在一个半球形的透明介质中的(如图所示)有一种用于电子显示屏的发光二极管,其管芯的发光区域为直径等于2mm的圆盘,封装用的透明介质的折射率为1.7,为了使人们能在更大的角度范围内最清晰的看到发光二极管发出的光,即要求管芯发光面上每一个发光点发出的光都能从整个半球面射出,试分析在制作发光管时半球形介质的半径R应满足是什么条件.
与小白炽灯泡和氖灯相比,发光二极管具有工作电压低(有的仅一点几伏),工作电流很小(有的仅零点几毫安即可发光)、抗冲击和抗震性能好、可靠性高、寿命长、通过调节电流可以方便地调节发光的强弱等特点,被广泛应用于电子显示屏和新型照明光源等领域,通常发光二极管的成品是将发光二极管的管芯封装在一个半球形的透明介质中的(如图所示)有一种用于电子显示屏的发光二极管,其管芯的发光区域为直径等于2mm的圆盘,封装用的透明介质的折射率为1.7,为了使人们能在更大的角度范围内最清晰的看到发光二极管发出的光,即要求管芯发光面上每一个发光点发出的光都能从整个半球面射出,试分析在制作发光管时半球形介质的半径R应满足是什么条件. 如图所示,静止的气缸内封闭了一定质量的气体,水平轻杆一端固定在墙壁上,另一端与气缸内的活塞固定相连.已知大气压强为1.0×105Pa,气缸的质量为50kg,活塞质量不计,其横截面积为0.01m2,气缸与地面间的最大静摩擦力为气缸重力的0.4倍,活塞与气缸之间的摩擦可忽略.开始时被封闭的气体压强为1.0×105Pa、温度为27℃,气缸静止.求:改变被封闭气体的温度最大在什么范围内可保证气缸静止不动.
如图所示,静止的气缸内封闭了一定质量的气体,水平轻杆一端固定在墙壁上,另一端与气缸内的活塞固定相连.已知大气压强为1.0×105Pa,气缸的质量为50kg,活塞质量不计,其横截面积为0.01m2,气缸与地面间的最大静摩擦力为气缸重力的0.4倍,活塞与气缸之间的摩擦可忽略.开始时被封闭的气体压强为1.0×105Pa、温度为27℃,气缸静止.求:改变被封闭气体的温度最大在什么范围内可保证气缸静止不动.
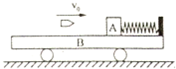 如图所示,质量M=9kg小车B静止在光滑水平面上,小车右端固定一轻质弹簧,质量m=0.9kg的木块A(可视为质点)紧靠弹簧放置并处于静止状态,A与弹簧不栓接,弹簧处于原长状态.木块A右侧车上表面光滑,木块A左侧车表面粗糙,动摩擦因数μ=0.75.一颗质量m0=0.1kg的子弹以v0=100m/s的速度水平向右飞来,瞬间击中木块并留在其中.如果最后木块A刚好不从小车左端掉下来,
如图所示,质量M=9kg小车B静止在光滑水平面上,小车右端固定一轻质弹簧,质量m=0.9kg的木块A(可视为质点)紧靠弹簧放置并处于静止状态,A与弹簧不栓接,弹簧处于原长状态.木块A右侧车上表面光滑,木块A左侧车表面粗糙,动摩擦因数μ=0.75.一颗质量m0=0.1kg的子弹以v0=100m/s的速度水平向右飞来,瞬间击中木块并留在其中.如果最后木块A刚好不从小车左端掉下来,