Question

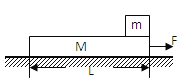
【题目】如图所示，光滑水平面上放着长为L＝25m，质量为M=5kg的木板（厚度不计），一个质量为m=1kg的小物体放在木板的最右端，m和M之间的动摩擦因数μ=0.1，开始均静止。今对木板施加一水平向右的恒定拉力F=21N，作用2s后，撤去拉力F，求：

（1）还没撤拉力F的过程小物块和木板的加速度各为多大

（2）整个过程木板和小物体因摩擦而产生的热量

Answer 1

【答案】（1）a1＝1 m/s2 ，a2＝4m/s2；（2）21J。

【解析】

（1）由题意知木块向右作匀加速运动，根据牛顿第二定律，对木块有：

则木块的加速度大小为：

；

对木板有：

则木板的加速度大小为：

；

（2）相对滑动的路程为

代入数据可得：

s1=6m

产生的热量

Q1=μmgs1

联立解得

Q1=6J

此时m的速度

υ1=a1t=2m/s，

υ2=a2t=4×2=8m/s

撤去拉力后，取向右为正方向，由动量守恒定律可知：

mυ1+Mυ2=(m+M)υ共

解得

υ共=7m/s

相对运动的时间

相对滑动的路程为

有：

所以m没有掉下去，能够和M共速度

由能量关系可知：

Q2=μmgs2

解得

Q2=15J

总热量为

Q总=Q1+Q2=21J