题目内容
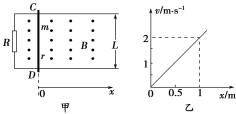
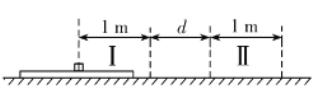
【题目】如图所示,质量为m=1kg,电量q=+10-4C的物块(可以看成质点),放置在质量M=2kg足够长的绝缘木板中间物块与木板间的动摩擦因数为μ=0.1,木板放置在光滑的水平地面上.在地面上方存在两个具有理想边界的电场区,两区域内的电场强度大小相等,均为E=3×104V/m,宽度均为L=1m,边界距离为d,Ⅰ区电场强度的方向水平向右,Ⅱ区的电场强度方向水平向左。将物块与木板从图示位置(物块在区内的最左边)由静止释放,已知在整个过程中物块不会滑离木板。取g=10m/s2。
(1)在物块刚离开Ⅰ区域时,物块的速度多大?
(2)若物块刚进入Ⅱ区域时,物块与木板的速度刚好相同,求两电场区的边界距离d;
(3)物块与木板最终停止运动时,求它们相对滑动的路程。
【答案】(1)2m/s;(2)1.5m;(3)3m
【解析】
(1) 对物块由牛顿第二定律
:![]()
由
![]()
得
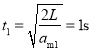
物块刚离开Ⅰ区域时,物块的速度
![]()
(2) Ⅰ区域内,对木板
![]()
物块到达Ⅰ区域边缘处,木板的速度
![]()
离开Ⅰ区域后,对物块
![]()
对木板
![]()
当物块与木板达到共同速度时
![]()
得
t2=1s
两电场区边界距离为
![]()
(3)由于
![]()
所以物块与木板最终只能停在两作用区之间,由全过程能量守恒与转化规律
![]()
得它们相对滑动的路程
![]()

练习册系列答案
相关题目