题目内容
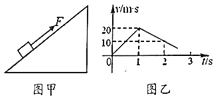
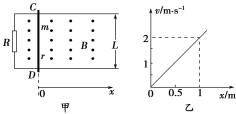
【题目】如图甲所示,左侧接有定值电阻R=2Ω的水平粗糙导轨处于垂直纸面向外的匀强磁场中,磁感应强度B=1T,导轨间距L=1m。一质量m=2kg,阻值r=2Ω的金属棒在水平拉力F作用下由静止开始从CD处沿导轨向右加速运动,金属棒的v-x图象如图乙所示,若金属棒与导轨间动摩擦因数μ=0.2,则从起点发生x=1m位移的过程中(g=10 m/s2)( )
A. 金属棒克服安培力做的功W1=0.25 J
B. 金属棒克服摩擦力做的功W2=5 J
C. 整个系统产生的总热量Q=4.25 J
D. 拉力做的功W=9.25 J
【答案】AC
【解析】
由速度图象得出v与x的关系式,由安培力公式得到FA与x的关系式,可知FA与x是线性关系,即可求出发生s=1m位移的过程中安培力做功WA=-![]() x,再根据动能定理求解拉力做功;根据能量守恒求解整个系统产生的总热量Q.
x,再根据动能定理求解拉力做功;根据能量守恒求解整个系统产生的总热量Q.
由速度图象得:v=2x,金属棒所受的安培力![]() ,代入得:FA=0.5x,则知FA与x是线性关系。当x=0时,安培力FA1=0;当x=1m时,安培力FA2=0.5N,则从起点发生x=1m位移的过程中,安培力做功为:WA=-
,代入得:FA=0.5x,则知FA与x是线性关系。当x=0时,安培力FA1=0;当x=1m时,安培力FA2=0.5N,则从起点发生x=1m位移的过程中,安培力做功为:WA=-![]() x=-0.25J;即金属棒克服安培力做的功为:W1=0.25J,故A正确。金属棒克服摩擦力做的功为:W2=-μmgx=-0.2×2×10×1J=-4J,故B错误;克服安培力做功等于产生的电热,克服摩擦力做功等于产生的摩擦热,则整个系统产生的总热量Q=WA+W2=4.25 J,选项C正确;根据动能定理得:WF+W2+WA=
x=-0.25J;即金属棒克服安培力做的功为:W1=0.25J,故A正确。金属棒克服摩擦力做的功为:W2=-μmgx=-0.2×2×10×1J=-4J,故B错误;克服安培力做功等于产生的电热,克服摩擦力做功等于产生的摩擦热,则整个系统产生的总热量Q=WA+W2=4.25 J,选项C正确;根据动能定理得:WF+W2+WA=![]() mv2,其中v=2m/s,μ=0.2,m=2kg,代入解得拉力做的功为:WF=8.25J。故D错误。故选AC。
mv2,其中v=2m/s,μ=0.2,m=2kg,代入解得拉力做的功为:WF=8.25J。故D错误。故选AC。

练习册系列答案
相关题目