题目内容
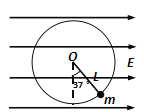
【题目】如图,长度L=0.4m的细线,拴着一个质量m=0.2kg的小球,在竖直平面内做圆周运动,O为圆心,A为小球做圆周运动的最低点,O点离地面高度h=1.2m,当小球经过A点时细线受到的拉力F=10N,g取10m/s2,求:
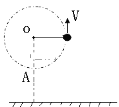
(1)小球在A点速度的大小VA;
(2)小球通过A点后能否通过竖直平面的最高点?若小球能通过竖直平面圆周的最高点,此时细线受到拉力多大;
(3)若小球运动到最低点A时细线恰好断裂,求细线断裂后小球飞行的水平距离。
【答案】(1)4m/s(2)不能(3)1.6m
【解析】
根据牛顿第二定律可求小球在最低点和最高点的速度,在A点细线断裂后做平抛运动,由平抛运动规律可得小球飞行的水平距离。
(1)小球在A点由牛顿第二定律有:F-mg=m![]()
解得小球在A点速度:vA=4m/s
(2)小球通过最高点的最小速度为v,由牛顿第二定律得:mg=m![]()
解得:v=2m/s
小球在最低点的能量为E1=![]() mvA2=1.6J
mvA2=1.6J
若小球通过最高点的能量为E2=![]() mv2+mg2L=2J
mv2+mg2L=2J
由于E1小于E2,所以小球不能过竖直平面圆周的最高点。
(3)细线断裂后小球做平抛运动有:
h-L=![]() gt2
gt2
x=vAt
解得细线断裂后小球飞行的水平距离:x=1.6m

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目