题目内容
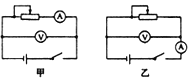
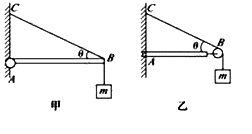
【题目】如图1所示,为“探究加速度与力、质量的关系”实验装置,获得了小车加速度a与沙及沙桶的质量及小车和砝码的质量对应关系图。沙桶和沙子的总质量为m1,小车和车上砝码的总质量为m2,重力加速度为g。


(1)实验中打点计时器所用电源的频率为50Hz,打出的其中一条纸带如图所示,由该纸带可求得小车的加速度a=________ m/s2。(结果保留两位有效数字)
(2)实验时,某同学由于疏忽,遗漏了平衡摩擦力这一步骤,测得![]() ,作出
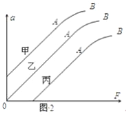
,作出![]() 图像,他可能作出图2中________ (选填“甲”、“乙”、“丙”)图线。此图线的AB段明显偏离直线,造成此误差的主要原因是________________________________________。
图像,他可能作出图2中________ (选填“甲”、“乙”、“丙”)图线。此图线的AB段明显偏离直线,造成此误差的主要原因是________________________________________。
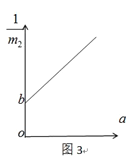
(3)实验时,某同学遗漏了平衡摩擦力这一步骤,若轨道水平,他测量得到的![]() 图像,如图3。设图中直线的斜率为k,在纵轴上的截距为b,则小车与木板间的动摩擦因数
图像,如图3。设图中直线的斜率为k,在纵轴上的截距为b,则小车与木板间的动摩擦因数![]() =________,沙桶和沙子的总质量
=________,沙桶和沙子的总质量![]() =________。(认为绳的拉力等于沙桶和沙子的总重力,忽略空气阻力及细线与滑轮的摩擦)
=________。(认为绳的拉力等于沙桶和沙子的总重力,忽略空气阻力及细线与滑轮的摩擦)
【答案】0.88 丙 没有满足m1远小于m2 ![]()
![]()
【解析】
(1)根据纸带可知,相邻计数点的时间间隔为:T=0.1s,根据△x=aT2得:![]()
(2)遗漏了平衡摩擦力这一步骤,就会出现当有拉力时,物体不动的情况.故图线为丙.
当不满足m1<<m2时,随m1的增大物体的加速度a逐渐减小,故图象弯曲的原因是:没有满足m1远小于m2.
(3)根据牛顿第二定律可知,m1g-μm2g=m2a;
结合![]() a图象,可得:
a图象,可得:![]() ,
,
设图中直线的斜率为k,在纵轴上的截距为b,因此![]() ,则钩码的质量m1=
,则钩码的质量m1=![]() ,小车与木板间的动摩擦因数μ=
,小车与木板间的动摩擦因数μ=![]() .
.

【题目】采用让重物自由下落的方法验证机械能守恒定律,实验装置如图所示:现有的器材为:带铁夹的铁架台、电火花打点计时器、纸带、重锤.

(1)需要测量物体由静止开始自由下落到某点时的瞬时速度v和下落高度h。某班同学利用实验得到的纸带,设计了以下四种测量方案,正确的是(_____)
A.用刻度尺测出物体下落的高度h,并测出下落时间t,通过v=gt计算出瞬时速度v
B.用刻度尺测出物体下落的高度h,并通过![]() 计算出瞬时速度v
计算出瞬时速度v
C.根据做匀变速直线运动时纸带上某点的瞬时速度,等于这点前后相邻两点间的平均速度,计算出瞬时速度v,并通过![]() 计算出高度h。
计算出高度h。
D.用刻度尺测出物体下落的高度h,根据做匀变速直线运动时纸带上某点的瞬时速度,等于这点前后相邻两点间的平均速度,计算出瞬时速度v。
(2)甲同学从打出的纸带中选出一条理想的纸带,如图所示。选取纸带上连续打出的5个点A、B、C、D、E,测出A点与起始点O的距离为s0,点A、C间的距离为s1,点C、E间的距离为s2。已知重锤的质量为m,打点计时器所接交流电的频率为f,当地的重力加速度为g。从起始点O开始到打下C点的过程中,重锤重力势能的减小量为△EP=__________,重锤动能的增加量为△EK=__________。在误差充许的范围内,如果△EP=△EK,则可验证机械能守恒。

(3)乙同学经正确操作得到打点纸带,在纸带后段每两个计时间隔取一个计数点,依次为1、2、3、4、5、6、7,测量各计数点到起始点的距离h,并正确求出打相应点时的速度v。各计数点对应的数据见下表:
计数点 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
h/m | 0.124 | 0.194 | 0.279 | 0.380 | 0.497 | 0.630 | 0.777 |
v/(m·s-1) | 1.94 | 2.33 | 2.73 | 3.13 | |||
v2/(m2·s-2) | 3.76 | 5.43 | 7.45 | 9.80 | 12.25 |
他在如图所示的坐标中,描点作出v2-h图线。由图线可知,重锤下落的加速度g′=__________m/s2(保留三位有效数字);若当地的重力加速度g=9.80m/s2,如果在误差允许的范围内g′=__________,则可验证机械能守恒。