题目内容
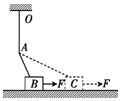
【题目】在竖直平面内有水平向右的匀强电场。在电场中有一根长为2m的绝缘细线,一端固定在O点,另一端系质量为0.04kg、带电荷量为3×10-5C的带电小球(视为质点),它静止时细线与竖直方向成37°角,如图所示。给小球一个初速度,让小球恰能绕O点在竖直平面内做圆周运动,取小球在静止时的位置为电势能和重力势能的零点,下列说法正确的是(取cos37°=0.8,g=10m/s2)( )
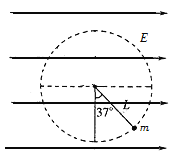
A.匀强电场的电场强度大小为2×104N/C
B.小球的动能最小值为0.96J
C.小球的机械能最小值为1.54J
D.小球运动过程中的最大电势能为0.96J
【答案】CD
【解析】
A.小球静止时有
![]()
代入解得
![]()
故A错误;
B.重力和电场力的合力为
![]()
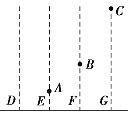
小球恰能绕O点在竖直平面内做圆周运动,其等效最高点为将绳反向延长与圆的交点,如图所示
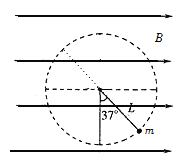
在等效最高点时动能最小,由F提供向心力可得
![]()
故动能的最小值为
![]()
故B错误;
C.电场力做负功最多时,机械能最小,故机械能最小的点为圆轨道,最左边的点,如图中C点
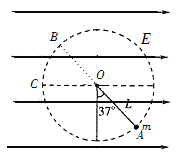
从A到C点,电场力做功为
![]()
在A点,小球机械能为
![]()
从A到B,由动能定理可得
![]()
故小球在C的机械能为
![]()
代入数据,解得
![]()
故C正确;
D.因为A点电势能为零,故小球在C时电势能最大
![]()
代入,解得
![]()
故D正确。
故选CD。

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目