题目内容
一玩具“火箭”由质量为ml和m2的两部分和压在中间的一根短而硬(即劲度系数很大)的轻质弹簧组成.起初,弹簧被压紧后锁定,具有的弹性势能为E0,通过遥控器可在瞬间对弹簧解除锁定,使弹簧迅速恢复原长。现使该“火箭”位于一个深水池面的上方(可认为贴近水面),释放同时解除锁定。于是,“火箭”的上部分竖直升空,下部分竖直钻入水中。设火箭本身的长度与它所能上升的高度及钻入水中的深度相比,可以忽略,但体积不可忽略。试求.
小题1:“火箭”上部分所能达到的最大高度(相对于水面) 小题2:若上部分到达最高点时,下部分刚好触及水池底部,那么,此过程中,“火箭”下部分克服水的浮力做了多少功?(不计水的粘滞阻力)
小题1: H1=v12/2g=m2E0/m1g(m1+m2) x
小题2:WF=E0
小题1:“火箭”整体(含弹簧)在弹簧解除锁定的瞬间,弹簧弹力远大于箭体重力,故动量守恒:m1v1-m2v2="0 "
同时机械能守恒:(m1v12)/2+(m2v22)/2=E0
∴v1=[2m2E0/m1(m1+m2)]

v2=[2m1E0/m2(m1+m2)]

∴“火箭”上部分所能达到的最大高度为:
H1=v12/2g=m2E0/m1g(m1+m2) x
小题2:“火箭”上升的时间为:t=v1/g
水池深度为:H2=v2t/2
“火箭”下部分克服水的浮力共做功:
WF=m2gH2+m2v22/2
以上各式联立可得:WF=E0

练习册系列答案
相关题目


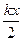 t=mv0 B
t=mv0 B 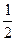 kx2=
kx2=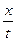 =
=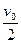 D 以上关系式均不正确
D 以上关系式均不正确