题目内容
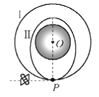
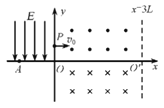
【题目】如图,在xOy平而内,x=0与x=3L两直线之间存在两匀强磁场,磁感应强度大小相同,方向均垂直于xOy平面,x轴为两磁场的分界线;在第I象限内存在沿y轴负方向、场强大小为E的匀强电场。一质量为m、电荷量为q(q>0)的粒子从x轴上的A点以某一初速度射入电场,一段时间后,该粒子运动到y轴上的P(0,![]() )点,以速度v0垂直于y轴方向进入磁场。不计粒子的重力。
)点,以速度v0垂直于y轴方向进入磁场。不计粒子的重力。
(1)求A点的坐标;
(2)若粒子能从磁场右边界离开,求磁感应强度的取值范围;
(3)若粒子能从O'(3L,0)点离开,求磁感应强度的可能取值。
【答案】(1)(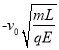 ,0);(2)
,0);(2)![]() ;(3)B可能的取值为
;(3)B可能的取值为![]() ,
,![]() ,
,![]()
【解析】
(1)粒子由A点到P点的运动可看成由P点到A点做类平抛运动,设运动时间为t,加速度大小为a,有
xA=v0t ①
qE=ma ②
![]() ③
③
由①②③得
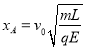 ④
④
A点的坐标为(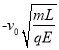 ,0)⑤
,0)⑤
(2)只要粒子不会从左边界离开,粒子就能到达右边界,设B的最大值为Bm,最小轨迹半径为R0,轨迹如答图a,图示的夹角为θ,则
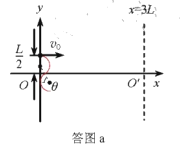
根据几何关系有
2R0cosθ=R0⑥
R0sinθ+R0=![]() ⑦
⑦
在磁场中由洛伦兹力提供向心力,则有
![]() ⑧
⑧
由⑥⑦⑧得
![]() ⑨
⑨
即磁感应强度的取值范围为
![]() ⑩
⑩
(3)设粒子到达O′点的过程中,经过x轴n次,一次到达x轴的位置与坐标原点O的距离为xn,如答图b,
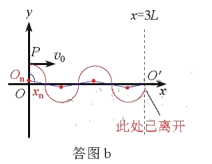
若粒子在第一次到达x轴的轨迹圆心角大于90°,即当![]() 时粒子将不可能到达O′点,故xn需要满足
时粒子将不可能到达O′点,故xn需要满足
![]()
且
(2n-1)xn=3L
故n只能取1、2、3(如答图c)
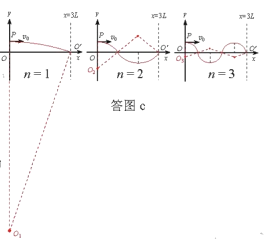
即x可能的取值为3L,L,![]()
又轨迹半径Rn满足
![]()
在磁场中由洛伦兹力提供向心力,则有
![]()
由得B可能取值为![]() ,
,![]() ,
,![]()

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目