题目内容
过山车是游乐场中常见的设施,下图是一种过山车的简易模型.它由水平轨道和在竖直平面内的若干个光滑圆形轨道组成,A、B、C…分别是各个圆形轨道的最低点,第一圆轨道的半径R1=2.0m,以后各个圆轨道半径均是前一轨道半径的k倍(k ="0.8)" ,相邻两最低点间的距离为两点所在圆的半径之和.一个质量m=1.0kg的物块(视为质点),从第一圆轨道的左侧沿轨道向右运动,经过A点时的速度大小为v0=12m/s.已知水平轨道与物块间的动摩擦因数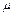 =0.5,水平轨道与圆弧轨道平滑连接. g取10m/s2,lg0.45=-0.347,lg0.8=-0.097.试求:
=0.5,水平轨道与圆弧轨道平滑连接. g取10m/s2,lg0.45=-0.347,lg0.8=-0.097.试求: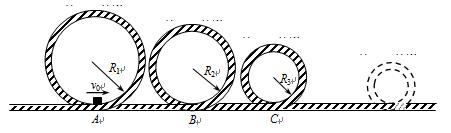
小题1:物块经过第一轨道最高点时的速度大小;
小题2:物块经过第二轨道最低点B时对轨道的压力大小;
小题3:物块能够通过几个圆轨道?
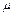 =0.5,水平轨道与圆弧轨道平滑连接. g取10m/s2,lg0.45=-0.347,lg0.8=-0.097.试求:
=0.5,水平轨道与圆弧轨道平滑连接. g取10m/s2,lg0.45=-0.347,lg0.8=-0.097.试求:
小题1:物块经过第一轨道最高点时的速度大小;
小题2:物块经过第二轨道最低点B时对轨道的压力大小;
小题3:物块能够通过几个圆轨道?
小题1:8m/s
小题2:77.5N
小题3:通过4个圆轨道
(1)设经第一个轨道最高点的速度为v,由机械能守恒有
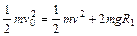
即有

(2)设物块经B点时的速度为vB,从A到B的过程由动能定理,
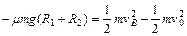
对物块经B点受力分析,由向心力公式有

联立两式解得

由牛顿第三定律可知,物块对轨道的压力大小为77.5N.
(3)设物块恰能通过第n个轨道,它通过第n个轨道的最高点时的速度为vn,有

对物块从A到第n个轨道的最高点的全过程由动能定理得
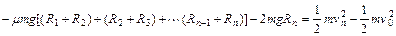
又因为
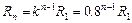
由以上三式可整理得
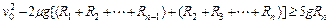
即
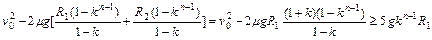
将v0=12m/s,
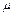 =0.5,R1=2m,k=0.8,g=10m/s2代入上式,整理得
=0.5,R1=2m,k=0.8,g=10m/s2代入上式,整理得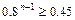 ,
,即有
 ,解得
,解得 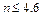
故物块共可以通过4个圆轨道.

练习册系列答案
相关题目
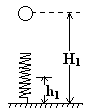
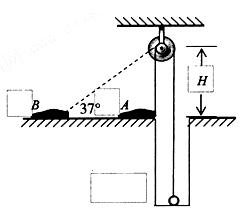
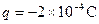 .如图14所示,开始时静止在场强
.如图14所示,开始时静止在场强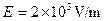 的匀强电场中的P点,靠近电场极板B有一挡板S,小球与挡板S的距离h =" 4" cm,与A板距离H =" 36" cm,小球的重力忽略不计.在电场力作用下小球向左运动,与挡板S相碰后电荷量减少到碰前的k倍,已知k = 7/8,碰撞过程中小球的机械能没有损失.
的匀强电场中的P点,靠近电场极板B有一挡板S,小球与挡板S的距离h =" 4" cm,与A板距离H =" 36" cm,小球的重力忽略不计.在电场力作用下小球向左运动,与挡板S相碰后电荷量减少到碰前的k倍,已知k = 7/8,碰撞过程中小球的机械能没有损失.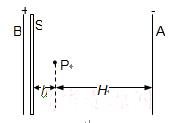
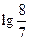 =0.058)
=0.058)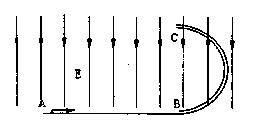
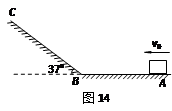
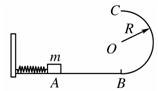
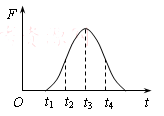
 水平面AB与竖直面内的半圆形导轨在B点相接,导轨
水平面AB与竖直面内的半圆形导轨在B点相接,导轨 半径为R.一个质量为m的物
半径为R.一个质量为m的物 体将弹簧压缩至A点后由静止释放,在弹力作用下物体获得某一向右速度后脱离弹簧,当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动恰能完成半个圆周运动到达C点.不计空气阻力.
体将弹簧压缩至A点后由静止释放,在弹力作用下物体获得某一向右速度后脱离弹簧,当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动恰能完成半个圆周运动到达C点.不计空气阻力.