Question

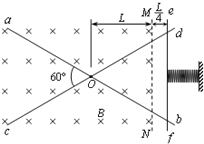
【题目】如图所示,光滑金属导体ab和cd水平固定,相交于O点并接触良好, =60° .一根轻弹簧一端固定,另一端连接一质量为m的导体棒ef,ef与ab和cd接触良好.弹簧的轴线与平分线重合.虚线MN是磁感应强度大小为B、方向竖直向下的匀强磁场的边界线,距O点距离为L.ab、cd、ef单位长度的电阻均为r.现将弹簧压缩t=0时,使ef从距磁场边界L/4处由静止释放,进入磁场后刚好做匀速运动,当ef到达O点时,弹簧刚好恢复原长,并与导体棒ef分离.已知弹簧形变量为x时,弹性势能为,k为弹簧的劲度系数.不计感应电流之间的相互作用.

(1)证明:导体棒在磁场中做匀速运动时,电流的大小保持不变;

(2)求导体棒在磁场中做匀速运动的速度大小v0和弹簧的劲度系数k;

(3)求导体棒最终停止位置距O点的距离.

Answer 1

【答案】（1），不变； (2) ，；（3）；

【解析】试题分析：设速度为v0，求解出电流的一般表达式分析即可；先根据棒加速过程中机械能守恒列式，再根据匀速过程受力平衡列式，联立后解方程组即可；从O点开始只受安培力，根据牛顿第二定律求出加速度的一般表达式，然后两边同时乘以时间间隔，最后将各个微元相加就可以得到结论。

(1)设匀速直线运动的速度为v0，ef有效切割长度为l，则电流: ，因为v0不变，所以I不变。

(2)由能量守恒得：

设弹簧形变量为x，由平衡条件得：

联立解得：

(3)ef越过O点后，与弹簧脱离，设导体棒最终停止位置距O点的距离为x0，某时刻回路中ef有效切割长度为L1，ef的速度为v，加速度为a，电流为I，

根据牛顿第二定律得：

电流

可得：

取一小段时间，速度微小变化为，回路面积微小增加为，则

即：

将代入得：