题目内容
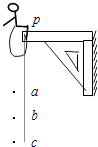
【题目】如图所示,某货场需将质量为m的货物(可视为质点)从高处运送至地面,现利用固定于地面的倾斜轨道传送货物,使货物由轨道顶端无初速滑下,轨道与水平面成θ=37°角.地面上紧靠轨道依次排放两块完全相同木板A、B,长度均为l=2m,厚度不计,质量均为m,木板上表面与轨道末端平滑连接.货物与倾斜轨道间动摩擦因数为μ0=0.125,货物与木板间动摩擦因数为μ1 , 木板与地面间动摩擦因数μ2=0.2.回答下列问题:(最大静摩擦力与滑动摩擦力大小相等,sin37°=0.6,cos37°=0.8,g=10m/s2)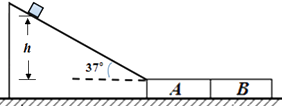
(1)若货物从离地面高h0=1.5m处由静止滑下,求货物到达轨道末端时的速度v0;
(2)若货物滑上木板A时,木板不动,而滑上木板B时,木板B开始滑动,求μ1应满足的条件;
(3)若μ1=0.5,为使货物恰能到达B的最右端,货物由静止下滑的高度h应为多少?
【答案】
(1)
解:货物在倾斜轨道上的受力如图,由牛顿第二定律:
mgsinθ﹣f=ma0,N﹣mgcosθ=0,
滑动摩擦力:f=Nμ0,
代入数据解得a0=5m/s2,由匀变速直线运动的速度位移公式得:
v02=2a0 ![]() ,
,
代入数据解得:v0=5m/s
(2)
解:若滑上木板A时,木板不动,由受力分析得:μ1mg≤μ2(m+2m)g,
若滑上木板B时,木板B开始滑动,由受力分析得:μ1mg>μ2(m+m)g,
代入数据得:0.4<μ1≤0.6
(3)
解:由(2)知货物滑上A时,木板不动,而滑上木板B时,木板B开始滑动.
货物下滑高度记为h2,到达斜道末端时速度记为v2,v22=2a0 ![]() ,
,
货物滑上A时做匀减速运动,加速度大小a1=gμ1=5m/s2
货物离开A时速度记为v3,v32﹣v22=﹣2a1l,
货物滑上B时,自身加速度大小a2=gμ1=5m/s2,
B的加速度大小a3=gμ1﹣2gμ2=1m/s2
由题意,货物到达B最右端时两者恰好具有共同速度,记为v4
货物做匀减速运动:v4=v3﹣a2t,v42﹣v32=﹣2a2l货,
B做匀加速运动:v4=a3t,v42=2a3lB,
位移关系满足:lB+l=l货,
代入数据解得:h2=2.64m
【解析】(1)货物下滑时根据牛顿第二定律求出下滑时的加速度,再根据速度位移关系求出到达末端时的速度;(2)根据木板动与不动的条件求解货物与木板间的动摩擦因数所满足的条件;(3)根据(2)中条件求解μ1=0.5时货物在A、B上运动情况由运动学公式求得货物静止时下滑的高度h.
【考点精析】掌握滑动摩擦力和匀变速直线运动的速度、位移、时间的关系是解答本题的根本,需要知道滑动摩擦力:利用公式f=μF N 进行计算,其中FN 是物体的正压力,不一定等于物体的重力,甚至可能和重力无关.或者根据物体的运动状态,利用平衡条件或牛顿定律来求解;速度公式:V=V0+at;位移公式:s=v0t+1/2at2;速度位移公式:vt2-v02=2as;以上各式均为矢量式,应用时应规定正方向,然后把矢量化为代数量求解,通常选初速度方向为正方向,凡是跟正方向一致的取“+”值,跟正方向相反的取“-”值.