��Ŀ����
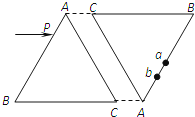
����Ŀ����ͼ��һ�̶�����ֱ������һ��һС����ͬ��ԲͲ��ɣ���ԲͲ�и���һ����������֪�����������Ϊm1=2.50kg��������Ϊs1=80.0cm2 �� С����������Ϊm2=1.50kg��������Ϊs2=40.0cm2���������ø���������ӣ���ౣ��Ϊl=40.0cm2 �� ���������ѹǿΪp=1.00��105Pa���¶�ΪT=303K����ʼʱ��������ԲͲ�ײ���� ![]() ������������������¶�ΪT1=495K���������������¶Ȼ����½��������������ƣ����������������ױ�֮���Ħ�����������ٶ�gȡ10m/s2 �� ��
������������������¶�ΪT1=495K���������������¶Ȼ����½��������������ƣ����������������ױ�֮���Ħ�����������ٶ�gȡ10m/s2 �� ��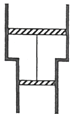
��1���ڴ�������ԲͲ�ײ��Ӵ�ǰ��˲�䣬���ڷ��������¶ȣ�
��2�����ڷ�յ��������������ﵽ��ƽ��ʱ�����ڷ�������ѹǿ��
���𰸡�
��1��
�⣺���ʼʱ�������ΪV1���ڴ�������ԲͲ�ײ��սӴ�ʱ�����ڷ����������ΪV2���¶�ΪT2������������� ![]() ��
��
V2=s2l��
�ڻ����������ƵĹ����У���pl��ʾ���������ѹǿ��������ƽ��������s1��p1��p��=m1g+m2g+s2��p1��p����
�ʸ��������ѹǿ���䣮�ɸǩ������˶����� ![]() ��
��
�����٢ڢ�ʽ������������ݵ�T2=330K��
���ڴ�������ԲͲ�ײ��Ӵ�ǰ��˲�䣬���ڷ��������¶�Ϊ330K��
��2��
�⣺�ڴ�������ԲͲ�ײ��սӴ�ʱ������������ѹǿΪp1���ڴ˺�������������ﵽ��ƽ��Ĺ����У�����������������䣮��ﵽ��ƽ��ʱ����������ѹǿΪp���ɲ������ɣ��� ![]() ��
��
�����ۢݢ�ʽ������������ݵ�p=1.01��105Pa
�𣺸��ڷ�յ��������������ﵽ��ƽ��ʱ�����ڷ�������ѹǿΪ1.01��105Pa
�����������⿼������������¶���ѹǿ�������������״̬�仯���̡�Ӧ�ø������˶�����������ɼ�����ȷ���⣮

 ��һ����ͬ���ɽ�����ϵ�д�
��һ����ͬ���ɽ�����ϵ�д� ������Ӧ���ϵ�д�
������Ӧ���ϵ�д� ��ʦ�㾦�ִʾ��ƪϵ�д�
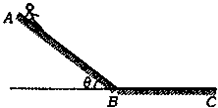
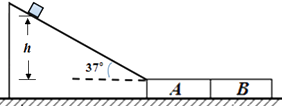
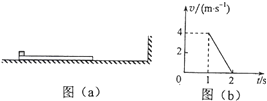
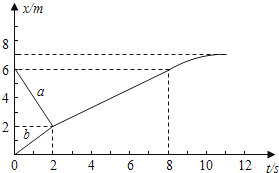
��ʦ�㾦�ִʾ��ƪϵ�д�����Ŀ��ij����С���ͬѧ�����һ���ֲ����С��ͨ����������͵�ʱ���ٶȵ�ʵ�飮���������У����С����ѹ��ʽ���̳ӡ�������ģ������Բ�����ֵİ뾶ΪR=0.20m�������������գ�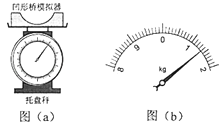
��1����������ģ�������������̳��ϣ���ͼ��a����ʾ�����̳ӵ� ʾ��Ϊ��
��2�������С�������ڰ�����ģ������͵�ʱ�����̳ӵ�ʾ����ͼ��b����ʾ����ʾ��Ϊkg��
��3����С���Ӱ�����ģ����ijһλ���ͷţ�С��������͵������һ�࣮�˹��������̳ӵ����ʾ��Ϊm����δ�ͬһλ���ͷ�С������¼���ε�mֵ���±���ʾ��
��� | 1 | 2 | 3 | 4 | 5 |
m��kg�� | 1.80 | 1.75 | 1.85 | 1.75 | 1.90 |
�����������ݣ������С��������������͵�ʱ���ŵ�ѹ��ΪN��С��ͨ����͵�ʱ���ٶȴ�СΪ m/s�����������ٶȴ�Сȡ9.80m/s2 �� ����������2λ��Ч���֣�