��Ŀ����
����Ŀ����ͼ��ʾ�������㹻���Ĺ⻬��������MN��PQ���ΪL=1.0m������費�ƣ������켰�乹�ɵ�ƽ�����ˮƽ���30��ǣ���ȫ��ͬ����������ab��cd�ֱ�ֱ������ã�ÿ�������˶��뵼��ʼ�������ýӴ�����֪������������Ϊm=0.02kg�������ΪR=0.2��������װ�ô��ڴ�ֱ�ڵ���ƽ�����ϵ���ǿ�ų��У��Ÿ�Ӧǿ�ȴ�СΪB=0.5T����ab��ƽ���ڵ������ϵ���F�����£��ص������������˶�������cdǡ���ܱ��־�ֹ��ȡg=10m/s2 �� ��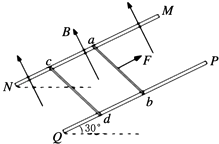
��1��ͨ��cd���ĵ���I�Ĵ�С��
��2����ab�ܵ�����F�Ĵ�С��
��3��������ͨ����·�����Ľ�����ΪQ=0.3Jʱ����F���Ĺ�W�Ƕ��٣�
���𰸡�
��1���⣺��cd�ܵ��İ�����Ϊ��Fcd=ILB��
��cd�ڹ�����������ƽ�⣬���У�Fcd=mg sin30�㣬
��ã�I=0.2A��
��ͨ��cd���ĵ���I�Ĵ�СΪ0.2A��
��2���⣺��ab���cd�ܵ��İ�������С��ȣ��У�Fab=Fcd��
��ab�ɹ�����ƽ���У�F=mg sin30��+ILB��
�������ݽ�ã�F=0.2N��
�𣺰�ab�ܵ�����F�Ĵ�С0.2N��
��3���⣺����ʱ��t�ڵ�·�����Ľ�����ΪQ=0.3J�����cd����Q��=0.15J������
�ɽ������ɿ�֪ Q��=I2Rt��
��ab�������˶����ٶȴ�СΪv��������ĸ�Ӧ�綯��Ϊ��E=BLv��
�ɱպϵ�·ŷķ����֪��I= ![]() ��
��
��ʱ��t�ڣ���ab�ص����λ��Ϊ��x=vt��
��F���Ĺ�Ϊ��W=Fx��
�ۺ�������ʽ���������ݽ�ã�W=0.6J��
�𣺵�����ͨ����·�����Ľ�����Ϊ0.3Jʱ����F���Ĺ�W��0.6J��
����������1����cd���ݹ�������ƽ������������ǿ�ȣ���2����ab���cd�ɹ�����ƽ���з�������ab�ܵ�����F�Ĵ�С����3�����ݽ������ɡ������ڵ�Ÿ�Ӧ���ɺͱպϵ�·��ŷķ��������ٶȴ�С���ٸ���λ��ʱ���ϵ���λ�ƣ�����W=Fx������F���Ĺ�W��
�����㾫����������Ҫ�����˽����������ݵ����֪ʶ�㣬��Ҫ���ս������ɣ�����ͨ�����������������������ƽ�������ȸ�����ĵ�������ȣ���ͨ��ʱ������Ȳ�����ȷ�����⣮

 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�