Question

【题目】如图所示，弧形轨道AB末端与水平左面在B点相切．质量m=0.5kg的小滑块，沿弧形轨道下滑，从B点以vB=2m/s的速度水平飞出．若桌面离地面高度h=0.45m，规定地面的重力势能为零，重力加速度g=10m/s2 ， 不计空气阻力．求：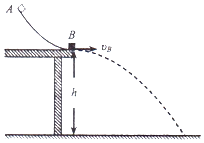

（1）小滑块从B点飞出到落地的时间；
（2）小滑块在B点的重力势能Ep；
（3）小滑块落地时的动能Ek ．

Answer 1

【答案】
（1）解：据平抛运动规律，竖直方向有：

h= gt2

得：t= = =0.3s

答：小滑块从B点飞出到落地的时间为0.3s；

（2）据重力势能公式有：Ep=mgh

得：EP=0.5×10×0.45=2.25J．

答：小滑块在B点的重力势能Ep为2.25J

（3）小滑块从B到落地，据机械能守恒定律有：

Ek=mgh+ m

解得：Ek=0.5×10×0.45+ ×0.5×4=3.25J．

答：小滑块落地时的动能Ek为3.25J．

【解析】本题考查机械能守恒定律以及平抛运动规律的应用，利用平抛运动竖直方向的运动可以计算时间，识记重力势能的表达式可以可算势能，要注意明确物体的运动过程，选取全过程机械能守恒定律，做好受力分析和运动过程分析，利用机械能守恒定律求解．
【考点精析】本题主要考查了平抛运动和机械能守恒及其条件的相关知识点，需要掌握特点:①具有水平方向的初速度;②只受重力作用，是加速度为重力加速度g的匀变速曲线运动；运动规律:平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动；在只有重力（和弹簧弹力）做功的情形下，物体动能和重力势能（及弹性势能）发生相互转化，但机械能的总量保持不变才能正确解答此题．