Question

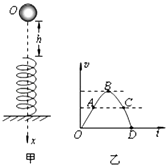
【题目】如图所示，B球静止在光滑水平面上，其左端连接得有一段轻弹簧；A球以3m/s的速度向B运动，已知A的质量2kg，B的质量1kg．

（1）整个过程中弹簧弹性势能最大值是多少？
（2）A与弹簧分离时，A、B的速度分别为多少？

Answer 1

【答案】
（1）

解：A、B共速时，弹簧的弹性势能最大，A、B碰撞过程动量守恒，以A的初速度方向为正方向，

由动量守恒定律得：mAv0=（mA+mB）v，

由机械能守恒定律得： ，

代入数据得：EP=3J

（2）

解：弹簧恢复原长时，B的速度最大，以A的初速度方向为正方向，

由动量守恒定律得：mAv0=mAvA+mBvB，

由机械能守恒定律得： ，

代入数据得：vA=1m/svB=4m/s

【解析】（1）A、B速度相等时，弹簧的弹性势能最大，由动量守恒定律与能量守恒定律可以求出最大弹性势能．（2）弹簧恢复原长时，B的速度最大，由动量守恒定律与机械能守恒定律可以求出A、B的速度．
【考点精析】根据题目的已知条件，利用动量守恒定律的相关知识可以得到问题的答案，需要掌握动量守恒定律成立的条件：系统不受外力或系统所受外力的合力为零；系统所受的外力的合力虽不为零，但系统外力比内力小得多；系统所受外力的合力虽不为零，但在某个方向上的分量为零，则在该方向上系统的总动量的分量保持不变．