题目内容
【题目】如图所示，物体A和带负电的物体B用跨过定滑轮的绝缘轻绳连接，A、B的质量分别是m和2m，劲度系数为k的轻质弹簧一端固定在水平面上，另一端与物体A相连，倾角为θ的斜面处于沿斜面向上的匀强电场中，整个系统不计一切摩擦．开始时，物体B在一沿斜面向上的外力F=3mgsinθ的作用下保持静止且轻绳恰好伸直，然后撤去外力F，直到物体B获得最大速度，且弹簧未超过弹性限度，则在此过程中（ ）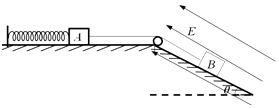
A.撤去外力F的瞬间，物体A的加速度为gsinθ
B.撤去外力F的瞬间，物体B的加速度为 
C.A，B获得最大速度时，弹簧伸长量为 
D.物体A和弹簧组成的系统机械能守恒
【答案】A,C
【解析】解：AB、当施加外力时，对B分析可知F﹣2mgsinθ﹣F电=0
解得F电=mgsinθ
当撤去外力瞬间，A和B的加速度相同，它们受到的合力为F合=F电+2mgsinθ=（m+2m）a
解得：a=gsinθ，A符合题意、B不符合题意；
C、当B受到的合力为零时，B的速度最大，由kx=F电+2mgsinθ解得x= 
，C符合题意；
D、绳子拉力对A做正功，A和弹簧组成的系统机械能是增大的，D不符合题意；
故答案为：AC．
对B物体受力分析，求的电场力，由牛顿第二定律求的加速度，当B受到的合力为零时，速度最大，根据机械能守恒定律的守恒条件判断物体A和弹簧组成的系统机械能是否守恒．
练习册系列答案
导学全程练创优训练系列答案
相关题目
