题目内容
【题目】如图所示,足够长的光滑平板AP与BP用铰链连接,平板AP与水平面成53![]() 角固定不动,平板BP可绕水平轴在竖直面内自由转动,质量为m的均匀圆柱体O放在两板间,sin53
角固定不动,平板BP可绕水平轴在竖直面内自由转动,质量为m的均匀圆柱体O放在两板间,sin53![]() =0.8,cos53
=0.8,cos53![]() =0.6,重力加速度为g。在使BP板由水平位置缓慢转动到竖直位置的过程中,下列说法正确的是( )
=0.6,重力加速度为g。在使BP板由水平位置缓慢转动到竖直位置的过程中,下列说法正确的是( )

A.平板BP受到的最小压力为![]() mg
mg
B.平板BP受到的最大压力为mg
C.平板AP受到的最小压力为![]() mg
mg
D.平板AP受到的最大压力为mg
【答案】A
【解析】
A.圆柱体受重力,斜面AP的弹力F1和挡板BP的弹力F2,将F1与F2合成为F,如下图:圆柱体一直处于平衡状态,三个力中任意两个力的合力与第三个力等值、反向、共线,故F1与F2合成的合力F与重力等值、反向、共线;从图中可以看出,BP板由水平位置缓慢转动过程中,F1越来越大,F2先减小后增大;由几何关系可知,当F2的方向与AP的方向平行(即与F1的方向垂直)时,F2有最小值F2min=![]() mg,根据牛顿第三定律,平板BP受到的最小压力为
mg,根据牛顿第三定律,平板BP受到的最小压力为![]() mg,故A正确。
mg,故A正确。
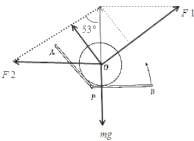
B.BP板由水平位置缓慢转动到竖直位置时,由图知这时F2最大,F2max=![]() mg,即平板BP受到的最大压力为
mg,即平板BP受到的最大压力为![]() mg,故B错误。
mg,故B错误。
C.当平板BP沿水平方向时,平板AP对圆柱体的弹力F1=0,即平板AP受到的最小压力为0,故C错误。
D.由图可知,当BP转到竖直方向时,AP对圆柱体的弹力F1最大,F1max=![]() =
=![]() mg,根据牛顿第三定律知,平板AP受到的最大压力为
mg,根据牛顿第三定律知,平板AP受到的最大压力为![]() mg,故D错误。
mg,故D错误。

练习册系列答案
相关题目