题目内容
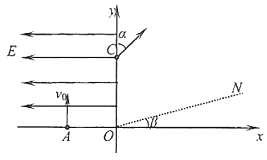
【题目】如图所示，在平面直角坐标系xOy中的第一象限内，存在磁感应强度大小为B、方向垂直于坐标平面向里的有界矩形匀强磁场区域（图中未画出）；在第二象限内存在沿x轴负方向的匀强电场。一粒子源固定在x轴上坐标为
的A点。粒子源沿y轴正方向释放出一个速率为
的电子，电子通过y轴上的C点时，速度方向与y轴正方向成 
＝45°角，电子经过磁场偏转后从D点（图中未画出）离开磁场，之后恰好垂直通过第一象限内与x轴正方向成 
15°角的射线ON．已知电子的质量为m，电荷量值为e，不考虑电子的重力。求
（1）匀强电场的电场强度E的大小；
（2）电子在电场和磁场中运动的总时间t；
（3）C、D两点间的距离。
【答案】(1)
；(2)
；(3)
【解析】
电子从A到C的过程中，由动能定理得：
且
联立解得：
；
电子在电场中做类平抛运动，沿电场方向有：
，
其中
由数学知识知电子在磁场中的速度偏向角等于圆心角：
电子在磁场中的运动时间：
，
其中
电子在电场和磁场中运动的总时间
联立解得：
；
电子在磁场中做匀速圆周运动，洛伦兹力提供向心力，
则有
磁场存在的最小矩形区域如图所示。
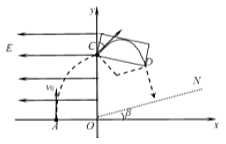
由数学知识得：
联立解得：
。
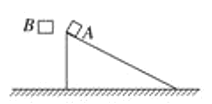
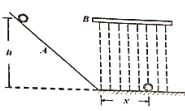
培优好卷单元加期末卷系列答案
【题目】为了研究物体的动能与物体的质量有怎样的关系，某实验小组设计了这样一个实验： 装置如图所示，将质量不同的小球从光滑斜面上同一高度处由静止释放，小球到达水平面时，立即遇到一系列条形布帘阻挡，经过一定的位移x后停下。因为布帘对小球的阻力恒定，所以每次小球克服阻力所作的功都与x成正比，他们记录了每次实验小球的质量m和小球的位移x，如下表所示：
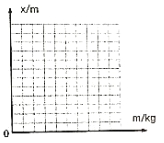
m（kg） | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 |
x（m） | 0.08 | 0.16 | 0.23 | 0.32 | 0.41 |
请回答下列问题：
(1)实验中，每次小球释放的高度总是相同的，这样做的目的是______________；
(2)在图中两出x-m图像_________________；
(3)根据图像可以得出x与m的数学表达式为：_________________，你认为决定图像的斜率大小的因素可能是___________________。
