题目内容
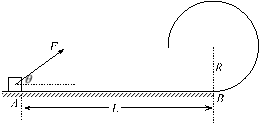
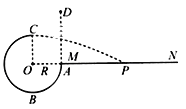
【题目】如图所示，竖直放置的半圆形轨道与水平轨道平滑连接，不计一切摩擦。圆心O点正下方放置为2m的小球A，质量为m的小球B以初速度v0向左运动，与小球A发生弹性碰撞。碰后小球A在半圆形轨道运动时不脱离轨道，则小球B的初速度v0可能为（ ）
A. 
B. 
C. 
D. 
【答案】BC
【解析】A与B碰撞的过程为弹性碰撞，则碰撞的过程中动量守恒，设B的初速度方向为正方向，设碰撞后B与A的速度分别为v1和v2，则：
mv0=mv1+2mv2
由动能守恒得：
联立得： 
①
1.恰好能通过最高点,说明小球到达最高点时小球的重力提供向心力,是在最高点的速度为vmin，由牛顿第二定律得：
2mg= 
②
A在碰撞后到达最高点的过程中机械能守恒，得：
③
联立①②③得：v0=
，可知若小球B经过最高点，则需要：v0
2.小球不能到达最高点，则小球不脱离轨道时，恰好到达与O等高处，由机械能守恒定律得：
④
联立①④得：v0=
可知若小球不脱离轨道时,需满足：v0
由以上的分析可知,若小球不脱离轨道时,需满足：v0
或v0
，故AD错误，BC正确。
故选：BC
练习册系列答案
相关题目
