题目内容
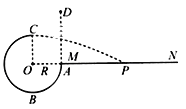
【题目】如图所示,半径为R的光滑圆弧轨道ABC固定在竖直平面内,O是圆心,OC竖直,OA水平,B是最低点,A点紧靠一足够长的平台MN,D点位于A点正上方,DA距离为有限值.现于D点无初速度释放一个大小可以忽略的小球,在A点进入圆弧轨道,从C点飞出后做平抛运动并落在平台MN上,P点是小球落在MN之前轨迹上紧邻MN的一点,不计空气阻力,下列说法正确的是()
A. 只要D点的高度合适,小球可以落在平台MN上任意一点
B. 小球从A运动到B的过程中,重力的功率一直增大
C. 小球由D经A,B,C到P的过程中,其在D点的机械能大于P点的机械能
D. 如果DA距离为h,则小球经过B点时对轨道的压力为
【答案】D
【解析】
A、小球恰好通过C点时，有mg=m
，vC=
，小球离开C点后做平抛运动，由R=
，得t=
，平抛运动的水平距离最小值x=vCt=
R，所以小球只有落在平台MN上距M点距离为（-1）R的右侧位置上，故A错误。
B、小球从A运动到B的过程中，在B点，重力与速度垂直，重力的瞬时功率为0，所以小球到达B点前重力的功率在减小，故B错误。
C、小球由D经A，B，C到P的过程中，只有重力做功，机械能守恒，则其在D点的机械能等于P点的机械能，故C错误。
D、小球从D运动到B的过程中，由机械能守恒得：mg（h+R）=
，在B点，由牛顿第二定律得：N-mg=m
，解得：N=3mg+
，由牛顿第三定律得知，小球经过B点时对轨道的压力N′=N=3mg+．故D正确。故选D。
练习册系列答案
相关题目
