题目内容
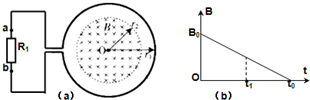
（2009?广东）如图（a）所示，一个电阻值为R，匝数为n的圆形金属线圈与阻值为2R的电阻R
1连接成闭合回路，线圈的半径为r
1，在线圈中半径为r
2的圆形区域内存在垂直于线圈平面向里的匀强磁场，磁感应强度B随时间t变化的关系图线如图（b）所示，图线与横、纵轴的截距分别为t
0和B
0导线的电阻不计，求0至t
1时间内
（1）通过电阻R
1上的电流大小和方向；
（2）通过电阻R
1上的电量q及电阻R
1上产生的热量．
分析：（1）由B-t图象的斜率读出磁感应强度的变化率
，由法拉第电磁感应定律求出线圈中产生的感应电动势，由欧姆定律求出感应电流的大小，由楞次定律判断出感应电流的方向．
（2）由公式q=It求出通过电阻R
1上的电量q，由焦耳定律求出电阻R
1上产生的热量．
解答：解：（1）由图象分析可知，0至t
1时间内
=
由法拉第电磁感应定律有E=n
=n
s
而s=
π由闭合电路欧姆定律有
I1=联立以上各式解得
通过电阻R
1上的电流大小为
I
1=
由楞次定律可判断通过电阻R
1上的电流方向为从b到a．
（2）通过电阻R
1上的电量q=I
1t
1=
通过电阻R
1上产生的热量为 Q=
R1t1=
答：（1）通过电阻R
1上的电流大小为
，方向为从b到a；
（2）通过电阻R
1上的电量q=
，电阻R
1上产生的热量为
．
点评：本题是法拉第电磁感应定律、欧姆定律、焦耳定律的综合应用，应用法拉第定律时要注意s是有效面积，并不等于线圈的面积．
练习册系列答案
相关题目
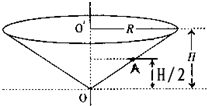（2009?广东）如图所示，一个竖直放置的圆锥筒可绕其中心轴OO′转动，同内壁粗糙，筒口半径和筒高分别为R和H，筒内壁A点的高度为筒高的一半，内壁上有一质量为m的小物块，求：
（2009?广东）如图所示，一带负电粒子以某速度进入水平向右的匀强电场中，在电场力作用下形成图中所示的运动轨迹．M和N是轨迹上的两点，其中M点在轨迹的最右点．不计重力，下列表述正确的是（ ）
（2009?广东）如图所示，在一个粗糙水平面上，彼此靠近地放置两个带同种电荷的小物块．由静止释放后，两个物块向相反方向运动，并最终停止．在物块的运动过程中，下列表述正确的是（ ）
（2009?广东）如图所示，绝缘长方体B置于水平面上，两端固定一对平行带电极板，极扳间形成匀强电场E，长方体B的上表面光滑，下表面与水平面的动摩擦因数μ=0.05（设最大静摩擦力与滑动摩擦力相同），B与极板的总质量mB=1.0kg．带正电的小滑块A质量mA=0.6kg，其受到的电场力大小F=1.2N．假设A所带的电量不影响极板间的电场分布．t=0时刻，小滑块A从B表面上的a点以相对地面的速度vA=1.6m/s向左运动，同时，B（连同极板）以相对地面的速度vB=0.40m/s向右运动．问（g取10m/s2）