题目内容
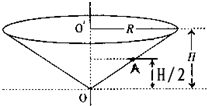 (2009?广东)如图所示,一个竖直放置的圆锥筒可绕其中心轴OO′转动,同内壁粗糙,筒口半径和筒高分别为R和H,筒内壁A点的高度为筒高的一半,内壁上有一质量为m的小物块,求:
(2009?广东)如图所示,一个竖直放置的圆锥筒可绕其中心轴OO′转动,同内壁粗糙,筒口半径和筒高分别为R和H,筒内壁A点的高度为筒高的一半,内壁上有一质量为m的小物块,求:①当筒不转动时,物块静止在筒壁A点受到的摩擦力和支持力的大小;
②当物块在A点随筒做匀速转动,且其所受到的摩擦力为零时,筒转动的角速度.
分析:(1)当筒不转动时,物块受到重力、筒壁A的摩擦力和支持力作用,根据平衡条件求解.角度由数学知识求出.
(2)当物块在A点随筒做匀速转动,且其受到的摩擦力为零时,由重力和支持力的合力提供物块的向心力,由牛顿第二定律求解.
(2)当物块在A点随筒做匀速转动,且其受到的摩擦力为零时,由重力和支持力的合力提供物块的向心力,由牛顿第二定律求解.
解答:解:(1)设圆锥母线与水平方向的夹角为θ.当筒不转动时,物块静止在筒壁A点时受到的重力、摩擦力和支持力三力作用而平衡,
由平衡条件得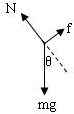
摩擦力的大小:f=mgsinθ=
支持力的大小:N=mgcosθ=
;
(2)当物块在A点随筒做匀速转动,且其所受到的摩擦力为零时,物块在筒壁A点时受到的重力和支持力作用,它们的合力提供向心力,设筒转动的角速度为ω有
mgtanθ=mω2

由几何关系得 tanθ=
联立解得ω=
答:(1)当筒不转动时,物块静止在筒壁A点受到的摩擦力为
,
支持力的大小为
;
(2)当物块在A点随筒做匀速转动,且其受到的摩擦力为零时,筒转动的角速度为
.
由平衡条件得

摩擦力的大小:f=mgsinθ=
| mgH | ||
|
支持力的大小:N=mgcosθ=
| mgR | ||
|
(2)当物块在A点随筒做匀速转动,且其所受到的摩擦力为零时,物块在筒壁A点时受到的重力和支持力作用,它们的合力提供向心力,设筒转动的角速度为ω有
mgtanθ=mω2
| R |
| 2 |

由几何关系得 tanθ=
| H |
| R |
| ||
| R |
答:(1)当筒不转动时,物块静止在筒壁A点受到的摩擦力为
| mgH | ||
|
支持力的大小为
| mgR | ||
|
(2)当物块在A点随筒做匀速转动,且其受到的摩擦力为零时,筒转动的角速度为
| ||
| R |
点评:本题是圆锥摆类型.关于向心力应用的基本方程是:指向圆心的合力等于向心力,其实是牛顿第二定律的特例.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
 (2009?广东)如图所示,一带负电粒子以某速度进入水平向右的匀强电场中,在电场力作用下形成图中所示的运动轨迹.M和N是轨迹上的两点,其中M点在轨迹的最右点.不计重力,下列表述正确的是( )
(2009?广东)如图所示,一带负电粒子以某速度进入水平向右的匀强电场中,在电场力作用下形成图中所示的运动轨迹.M和N是轨迹上的两点,其中M点在轨迹的最右点.不计重力,下列表述正确的是( ) (2009?广东)如图所示,在一个粗糙水平面上,彼此靠近地放置两个带同种电荷的小物块.由静止释放后,两个物块向相反方向运动,并最终停止.在物块的运动过程中,下列表述正确的是( )
(2009?广东)如图所示,在一个粗糙水平面上,彼此靠近地放置两个带同种电荷的小物块.由静止释放后,两个物块向相反方向运动,并最终停止.在物块的运动过程中,下列表述正确的是( )
 (2009?广东)如图所示,绝缘长方体B置于水平面上,两端固定一对平行带电极板,极扳间形成匀强电场E,长方体B的上表面光滑,下表面与水平面的动摩擦因数μ=0.05(设最大静摩擦力与滑动摩擦力相同),B与极板的总质量mB=1.0kg.带正电的小滑块A质量mA=0.6kg,其受到的电场力大小F=1.2N.假设A所带的电量不影响极板间的电场分布.t=0时刻,小滑块A从B表面上的a点以相对地面的速度vA=1.6m/s向左运动,同时,B(连同极板)以相对地面的速度vB=0.40m/s向右运动.问(g取10m/s2)
(2009?广东)如图所示,绝缘长方体B置于水平面上,两端固定一对平行带电极板,极扳间形成匀强电场E,长方体B的上表面光滑,下表面与水平面的动摩擦因数μ=0.05(设最大静摩擦力与滑动摩擦力相同),B与极板的总质量mB=1.0kg.带正电的小滑块A质量mA=0.6kg,其受到的电场力大小F=1.2N.假设A所带的电量不影响极板间的电场分布.t=0时刻,小滑块A从B表面上的a点以相对地面的速度vA=1.6m/s向左运动,同时,B(连同极板)以相对地面的速度vB=0.40m/s向右运动.问(g取10m/s2)