题目内容
(2009?广东)如图所示,水平地面上静止放置着物块B和C相距l=1.0m物快A以速度v0=10m/s沿水平方向与B正碰,碰撞后A和B牢固粘在一起向右运动,并再与C发生正碰,碰后瞬间C的速度v=2.0m/s,已知A和B的质量均为m.C的质量为A质量的k倍,物块与地面的动摩擦因数μ=0.45(设碰撞时间很短,g取10m/s2)

(1)计算与C碰撞前瞬间AB的速度
(2)根据AB与C的碰撞过程分析k 的取值范围,并讨论与C碰撞后AB的可能运动方向.

(1)计算与C碰撞前瞬间AB的速度
(2)根据AB与C的碰撞过程分析k 的取值范围,并讨论与C碰撞后AB的可能运动方向.
分析:该题要分清过程,过程Ⅰ为AB碰撞过程,该过程为完全非弹性碰撞过程;过程Ⅱ为AB粘在一块克服地面摩擦运动1m的过程,这一过程可由动能定理计算,也可由匀变速直线运动的知识计算,过程Ⅲ为可能是完全非弹性碰撞,也可能是弹性碰撞,也可能是完全弹性碰撞;根据不同的碰撞,AB、C系统损失的能量也不一样,所以AB球的方向可能与C同向、也可能为零、也可能与C反向.要分三种情况讨论
解答:解:(1)设AB碰撞后的速度为v1,AB碰撞过程由动量守恒定律得mv0=2mv1
设与C碰撞前瞬间AB的速度为v2,由动能定理得-μmgl=
m
-
m
联立以上各式解得v2=4m/s该过程为完全非弹性碰撞,
(2)若AB与C发生完全非弹性碰撞,由动量守恒定律得2mv2=(2+k)mv3
代入数据解得 k=2
此时AB的运动方向与C相同
若AB与C发生弹性碰撞,由动量守恒和能量守恒得
联立以上两式解得
代入数据解得 k=6
此时AB的运动方向与C相反
若AB与C发生碰撞后AB的速度为0,由动量守恒定律得2mv2=kmv
代入数据解得k=4
总上所述得 当2≤k<4时,AB的运动方向与C相同
当k=4时,AB的速度为0
当4<k≤6时,AB的运动方向与C相反.
设与C碰撞前瞬间AB的速度为v2,由动能定理得-μmgl=
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 1 |
联立以上各式解得v2=4m/s该过程为完全非弹性碰撞,
(2)若AB与C发生完全非弹性碰撞,由动量守恒定律得2mv2=(2+k)mv3
代入数据解得 k=2
此时AB的运动方向与C相同
若AB与C发生弹性碰撞,由动量守恒和能量守恒得
|
联立以上两式解得
|
代入数据解得 k=6
此时AB的运动方向与C相反
若AB与C发生碰撞后AB的速度为0,由动量守恒定律得2mv2=kmv
代入数据解得k=4
总上所述得 当2≤k<4时,AB的运动方向与C相同
当k=4时,AB的速度为0
当4<k≤6时,AB的运动方向与C相反.
点评:该题第一问较为简单,第二问稍难.只要注意到碰撞过程中能量个关系和动量守恒,这样就不会无从下手了

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
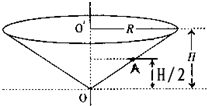 (2009?广东)如图所示,一个竖直放置的圆锥筒可绕其中心轴OO′转动,同内壁粗糙,筒口半径和筒高分别为R和H,筒内壁A点的高度为筒高的一半,内壁上有一质量为m的小物块,求:
(2009?广东)如图所示,一个竖直放置的圆锥筒可绕其中心轴OO′转动,同内壁粗糙,筒口半径和筒高分别为R和H,筒内壁A点的高度为筒高的一半,内壁上有一质量为m的小物块,求: (2009?广东)如图所示,一带负电粒子以某速度进入水平向右的匀强电场中,在电场力作用下形成图中所示的运动轨迹.M和N是轨迹上的两点,其中M点在轨迹的最右点.不计重力,下列表述正确的是( )
(2009?广东)如图所示,一带负电粒子以某速度进入水平向右的匀强电场中,在电场力作用下形成图中所示的运动轨迹.M和N是轨迹上的两点,其中M点在轨迹的最右点.不计重力,下列表述正确的是( ) (2009?广东)如图所示,在一个粗糙水平面上,彼此靠近地放置两个带同种电荷的小物块.由静止释放后,两个物块向相反方向运动,并最终停止.在物块的运动过程中,下列表述正确的是( )
(2009?广东)如图所示,在一个粗糙水平面上,彼此靠近地放置两个带同种电荷的小物块.由静止释放后,两个物块向相反方向运动,并最终停止.在物块的运动过程中,下列表述正确的是( ) (2009?广东)如图所示,绝缘长方体B置于水平面上,两端固定一对平行带电极板,极扳间形成匀强电场E,长方体B的上表面光滑,下表面与水平面的动摩擦因数μ=0.05(设最大静摩擦力与滑动摩擦力相同),B与极板的总质量mB=1.0kg.带正电的小滑块A质量mA=0.6kg,其受到的电场力大小F=1.2N.假设A所带的电量不影响极板间的电场分布.t=0时刻,小滑块A从B表面上的a点以相对地面的速度vA=1.6m/s向左运动,同时,B(连同极板)以相对地面的速度vB=0.40m/s向右运动.问(g取10m/s2)
(2009?广东)如图所示,绝缘长方体B置于水平面上,两端固定一对平行带电极板,极扳间形成匀强电场E,长方体B的上表面光滑,下表面与水平面的动摩擦因数μ=0.05(设最大静摩擦力与滑动摩擦力相同),B与极板的总质量mB=1.0kg.带正电的小滑块A质量mA=0.6kg,其受到的电场力大小F=1.2N.假设A所带的电量不影响极板间的电场分布.t=0时刻,小滑块A从B表面上的a点以相对地面的速度vA=1.6m/s向左运动,同时,B(连同极板)以相对地面的速度vB=0.40m/s向右运动.问(g取10m/s2)