��Ŀ����
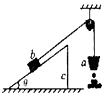
����Ŀ����ͼ��ʾ������ֱƽ���ڣ��뾶Ϊ2R���ķ�֮һԲ�����AB��뾶ΪR�İ�Բ���BC��B��ƽ�����ӣ�C��A������ͬ��ˮƽ���ϣ�C��B������ͬһ��ֱ���ϣ��е�ΪO����Բ��AB�ϵ�D����O��ȸߣ�һ������Ϊm��С����Ծ�A���ΪR��P���������䣬��A�������߽���Բ�����AB��ǡ��ͨ����ߵ�C����֪�������ٶ�Ϊg�����ƿ�����������С������˶������У� ��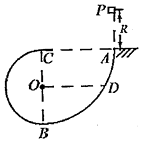
A.��P�㵽C�����������ΪmgR
B.��P�㵽C��˷�Ħ�������� ![]() mgR
mgR
C.����B��ǰ��˲�䣬С���Թ����ѹ������С
D.С����C��ɳ���Ӧ����Բ�����BD֮��
���𰸡�B
���������⣺A��С���ǡ��ͨ����ߵ�C���������ṩ���������� mg=m ![]() ���� vC=
���� vC= ![]()
��P�㵽C�㣬�ɶ��ܶ����ã����������� W��= ![]() ��0=
��0= ![]() mgR����A����
mgR����A����
B������W��=mgR��Wf �� �ÿ˷�Ħ�������� Wf= ![]() mgR����B��ȷ��
mgR����B��ȷ��
C������B��ǰ��˲�䣬С�������ʲ��䣬�����Ϊ�о�������ţ�ٵڶ����ɵã�N��mg=m ![]() ���� N=mg+m
���� N=mg+m ![]() �������뾶��С��������С����֧���������ţ�ٵ�������֪С���Թ����ѹ�������C����
�������뾶��С��������С����֧���������ţ�ٵ�������֪С���Թ����ѹ�������C����
D��С����C��ɳ�����ƽ���˶������� x=vCt��y= ![]()
���ɼ��ι�ϵ�� x2+y2=��2R��2 ��
��� t2= ![]() ��y=
��y= ![]() R��0.618R��R������С����C��ɳ���Ӧ����Բ�����AD֮�䣬��D����
R��0.618R��R������С����C��ɳ���Ӧ����Բ�����AD֮�䣬��D����
��ѡ��B
�����㾫����������Ŀ����֪����������ƽ���˶��������������֪ʶ���Եõ�����Ĵ𰸣���Ҫ�����ص�:�پ���ˮƽ����ij��ٶ�;��ֻ���������ã��Ǽ��ٶ�Ϊ�������ٶ�g���ȱ��������˶����˶�����:ƽ���˶����Էֽ�Ϊˮƽ���������ֱ���˶�����ֱ��������������˶�������������ָ��Բ�ģ��������ļ��ٶȣ�������ֻ�ı����ٶȵķ����ı��ٶȵĴ�С���������Ǹ�������Ч��������.�ڷ�����Բ���˶����ʵ��������ʱ��ǧ������������֮��������һ����������

 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д�