��Ŀ����
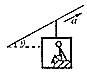
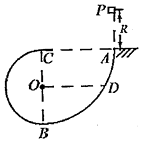
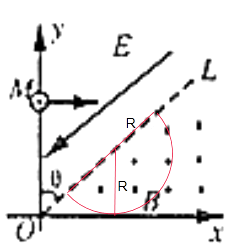
����Ŀ����ͼ��ʾ������OL��y��ļнǦ�=45�㣬��OL�ϲ���ƽ����OL���µ���ǿ�糡����OL�²��д�ֱֽ���������ǿ�ų���һ����Ϊm�������q��q��0��������������v0��y���ϵ�M��OM=d���㴹ֱ��y��������ǿ�糡��������ǡ���ܹ���ֱ��OL������ǿ�ų�����������������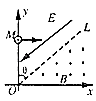
��1����˵糡�ij�ǿ��СE��
��2������������OL��x����Χ�����ڷ��ص�����OL�ϣ������Ӵ�M��������ڶ��ξ���OL����Ҫ���ʱ�䣮
���𰸡�
��1��
�⣺�����ڵ糡���˶�����������������ֻ�ܵ糡�����ã�F��=qE�� ![]() ��
��
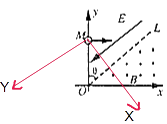
�ش�ֱ�糡�߷���X�͵糡�߷���Y��������ϵ��
����X����λ�ƹ�ϵ�У�dsin��=v0sin��t������ ![]() ��
��
������ǡ���ܹ���ֱ��OL������ǿ�ų���������Y�����ϣ��ٶȹ�ϵ�У�v0cos��=at= ![]() ��
��
���ԣ� ![]() ������
������ ![]()
��2��
�⣺���ݣ�1����֪�����ڵ糡���˶���ʱ�� ![]() ��
��
�����ڴų���ֻ���������������ã�������������������Բ���˶�����Բ���˶�������ΪT
��������OL��x����Χ�����ڷ��ص�����OL�ϣ������Ӵ�M��������ڶ��ξ���OL�ڴų����˶��˰��Բ�ܣ����ԣ��ڴų����˶�ʱ��Ϊ ![]() ��
��
�����ڴų��˶�������������Ϊ�������������У� ![]() ��
��
���ݣ�1����֪������ǡ���ܹ���ֱ��OL������ǿ�ų����ٶ�v���dz��ٶ�v0��X�����ϵķ������� ![]() ��
��
�����ڵ糡���˶�����Y�����ϵ�λ�� ![]() �����ԣ����ӽ���ų���λ����OL�Ͼ���O��
�����ԣ����ӽ���ų���λ����OL�Ͼ���O�� ![]() ��
��
���ݼ��ι�ϵ��
�ɵã� ![]() ����
���� 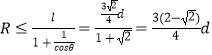 ��
��
���ԣ� 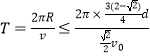 =
= ![]() ��
��
���ԣ����Ӵ�M��������ڶ��ξ���OL����Ҫ���ʱ�� ![]() =
= ![]()
����������1����������ֻ�ܵ糡�����ã��ص糡�߷���ʹ�ֱ�糡�߷���������ϵ��������ƽ���˶������ݺ���λ�Ƽ������ٶȽ��������飬������⣻��2���ɣ�1������ڵ糡���˶���ʱ�估�뿪�糡ʱ��λ�ã��ٸ��������ڴų�����Բ���˶�����Բ���˶����ɼ����ι�ϵ�õ����뾶�������õ��ʱ�䣻