题目内容
【题目】如图所示,固定斜面的倾角 ![]() ,物体 A 与斜面之间的动摩擦因数 μ=
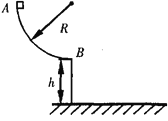
,物体 A 与斜面之间的动摩擦因数 μ=![]() ,轻弹簧下端固定在斜面底端,弹簧处于原长时上端位于 C 点。用一根不可伸长的轻绳通过轻质光滑的定滑轮连接物体 A和 B,滑轮右侧绳子与斜面平行,A 的质量为2m,B 的质量为m,初始时物体 A 到 C 点的距离为 L,现给 A、B 一初速度 v0使 A 开始沿斜面向下运动,B 向上运动,物体 A 将弹簧压缩到最短后又恰好能弹到 C 点。已知重力加速度为 g,不计空气阻力,整个过程中,轻绳始终处于伸直状态,求
,轻弹簧下端固定在斜面底端,弹簧处于原长时上端位于 C 点。用一根不可伸长的轻绳通过轻质光滑的定滑轮连接物体 A和 B,滑轮右侧绳子与斜面平行,A 的质量为2m,B 的质量为m,初始时物体 A 到 C 点的距离为 L,现给 A、B 一初速度 v0使 A 开始沿斜面向下运动,B 向上运动,物体 A 将弹簧压缩到最短后又恰好能弹到 C 点。已知重力加速度为 g,不计空气阻力,整个过程中,轻绳始终处于伸直状态,求

(1) 物体 A向下运动刚到 C点时的速度;
(2)弹簧的最大压缩量;
(3)弹簧的最大弹性势能。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)物体A向下运动到C点的过程中,A的重力势能及AB的动能都减小,转化为B的重力势能和摩擦生热,根据能量守恒定律列式求出物体A向下运动刚到C点时的速度;(2)从物体A接触弹簧到将弹簧压缩到最短后回到C点的过程中,弹簧的弹力和重力做功都为零,根据动能定理求出弹簧的最大压缩量;(3)弹簧从压缩最短到恰好能弹到C点的过程中,根据能量守恒定律求解弹簧中的最大弹性势能.
(1)A和斜面间的滑动摩擦力大小为![]() ,物体A向下运动到C点的过程中,根据功能关系有:
,物体A向下运动到C点的过程中,根据功能关系有:![]()
解得:![]()
(2)从物体A接触弹簧,将弹簧压缩到最短后又恰回到C点,对系统应用动能定理,有:![]()
解得:![]()
(3)弹簧从压缩最短到恰好能弹到C点的过程中,对系统根据能量关系有:![]()
因为![]()
所以有:![]()

练习册系列答案
相关题目