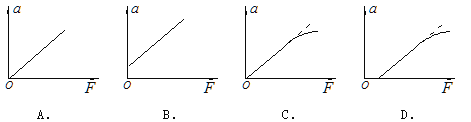题目内容
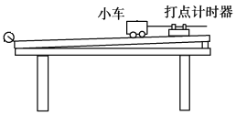
【题目】如图所示，某同学探究小车加速度与力的关系的实验装置，他将光电门固定在水平轨道上的B点，用不同重物通过细线拉同一小车，每次小车都从同一位置A由静止释放。
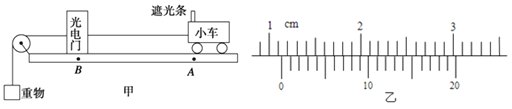
（1）若用游标卡尺测出遮光条的宽度d如图乙所示，则d= cm；实验时将小车从图示位置由静止释放，由数字计时器读出遮光条通过光电门的时间Δt=2．0×s，则小车经过光电门时的速度为 m/s；
（2）实验中可近似认为细线对小车的拉力与重物重力大小相等，则重物的质量m与小车的质量M间应满足的关系为 ;
（3）测出多组重物的质量m和对应遮光条通过光电门的时间Δt，并算出相应小车经过光电门时的速度v，通过描点作出线性图象，研究小车加速度与力的关系．处理数据时应作出 （选填“V-m”或“-m”）图象;
（4）某同学在（3）中作出的线性图象不通过坐标原点，其原因是 。
【答案】（1）1．140；0．57m/s（2）M远远大于m
（3）v2-m（4）小车与水平轨道间存在摩擦力（或未平衡摩擦力）
【解析】试题分析：（1）游标卡尺的主尺读数为11mm，游标读数为0．05×8mm=0．40mm，所以最终读数为：11mm+0．40mm=11．40mm=1．140cm；数字计时器记录通过光电门的时间，由位移公式计算出物体通过光电门的平均速度，用该平均速度代替物体的瞬时速度，故在遮光条经过光电门时滑块的瞬间速度为：
（2）该实验的研究对象是小车，采用控制变量法研究．当质量一定时，研究小车的加速度和小车所受合力的关系．为消除摩擦力对实验的影响，可以把木板右端适当垫高，以使小车的重力沿斜面分力和摩擦力抵消，那么小车的合力就是绳子的拉力．根据牛顿第二定律得，对m：
，对M：
，解得：
，当
时，即当重物重力要远小于小车的重力，绳子的拉力近似等于重物的总重力．
（3）由题意可知，该实验中保持小车质量M不变，因此有：
，由题意可知，M、s不变，画出v2-m图象，若图象为过原点的直线，则说明外力和加速度成正比，故画出v2-m图象可以直观的得出结论．
（4）开始当小车挂上重物时，加速度却为零，线性图象不通过坐标原点，故导致图象不过原点的原因是木板倾角偏小．即说明操作过程中没有平衡摩擦力或者平衡摩擦力不足．
