题目内容
如图所示，一个半球形的碗放在桌面上，碗口水平，O点为其球心，碗的内表面及碗口是光滑的，一根细线跨在碗口上，线的两端分别系有质量为m1和m2的小球，当它们处于平衡状态时，质量为m1的小球与O点的连线与水平线的夹角为α=60°，两小球的质量比| m1 |
| m1 |
分析：题中装置处于静止状态，两个小球的合力均为零．先对m2球受力分析，受重力和拉力，二力平衡，求出拉力；再对m1球受力分析，根据共点力平衡条件列式求解．
解答：解：m2球保持静止状态，对其受力分析，受重力和拉力，二力平衡，故
F=m2g ①
再对m1球受力分析，如图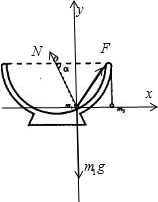
根据共点力平衡条件
x方向：Fcos60°-Ncos60°=0 ②
y方向：Fsin60°+Nsin60°-m1g=0 ③
由①②③代入数据解得：
=
=
故选：D．
F=m2g ①
再对m1球受力分析，如图
根据共点力平衡条件
x方向：Fcos60°-Ncos60°=0 ②
y方向：Fsin60°+Nsin60°-m1g=0 ③
由①②③代入数据解得：
| m1 |
| m2 |
| ||
| 1 |
| 3 |
故选：D．
点评：本题是简单的连接体问题，先分析受力最简单的物体，再分析受力较复杂的另一个物体，同时要运用正交分解法处理较为方便．
练习册系列答案
相关题目
如图所示，一个半球形的碗放在水平桌面上，碗口水平，O为其球心，碗的内表面及碗口是光滑的．一根细线跨在碗口上，线的两端分别系有质量为 m1的小球和质量为m2的物块，小球与O点的连线和水平线的夹角α=60°，设碗对小球的支持力大小为N，绳对小球的拉力大小为T（此时系统属于静止状态），则下列关系式正确的是（ ）
如图所示，一个半球形的碗放在桌面上，碗口水平，O是球心，碗的内表面光滑．一根轻质杆的两端固定有两个小球，质量分别是m1，m2．当它们静止时，m1、m2与球心的连线跟水平面分别成60°，30°角，则碗对两小球的弹力大小之比是（ ）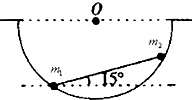
如图所示，一个半球形的碗放在桌面上，碗口水平，O点为其球心，碗的内表面是光滑的．一根质量可忽略的刚性细杆两端分别固定着质量为m1和m2的小球，放置在半球面内．已知细杆长度是球面半径的
如图所示，一个半球形的碗放在桌面上，碗口水平，O点为其球心，碗的内表面及碗口是光滑的．一根细线跨在碗口上，线的两端分别系有质量为m1和m2的小球，当它们处于平衡状态时，质量为m1的小球与O点的连线与水平线的夹角为α=60°．则两小球的质量比
如图所示，一个半球形的碗放在桌面上，碗口水平，O是球心，碗的内表面光滑．一根轻质杆的两端固定有两个小球，质量分别是m1，m2．当它们静止时，m1、m2与球心的连线跟水平面分别成60°，30°角，则碗对两小球的弹力大小之比是